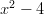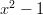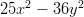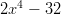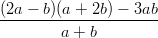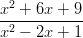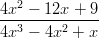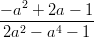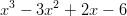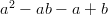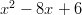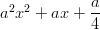Polynomit

Ensimmäisen asteen polynomi on muotoa ax + b oleva lauseke, toisen asteen polynomi on muotoa ax2 + bx + c, kolmannen asteen ax3 + bx2 + cx + d jne. Polynomissa voi olla myös useampia muuttujia, esimerkiksi ax2 + by2 + cxy + dx + ey + f.
Polynomilausekkeita esiintyy monissa yhteyksissä ja niitä joudutaan eri tavoin muokkaamaan. Tärkeimpiä operaatioita ovat sulkujen poisto (osittelulain avulla, esim. x2(ax2 + b) = ax4 + bx2), polynomin jako tekijöihin, kahden polynomin jakolasku jne.
 Polynomi
Polynomi Binomikaava
Binomikaava Polynomien jakolasku
Polynomien jakolasku Polynomien alkeellinen tekijöihin jako
Polynomien alkeellinen tekijöihin jako
Yhden muuttujan polynomifunktiolla on sille luonteenomaisia piirteitä, joiden tunteminen auttaa usein tilanteiden hahmottamista. Esimerkiksi toisen asteen polynomin kuvaaja on joko alaspäin tai ylöspäin aukeava paraabeli.

Esimerkkejä
- Erilaisten polynomifunktioiden kuvaajia:
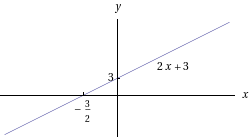
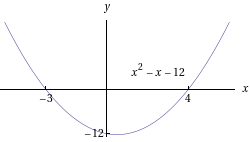
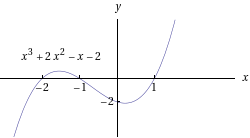
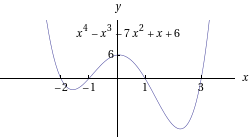
- Sievennetään kahden muuttujan polynomi:
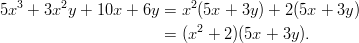
- Lasketaan binomikaavan avulla
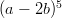 :
:
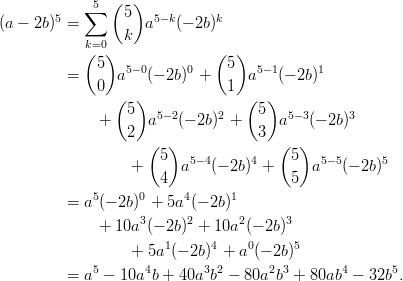
Toiseksi viimeisen rivin kertoimet saadaan myös Pascalin kolmion 5. riviltä.
- Neliöksi täydentämisessä pyritään löytämään sellainen summan
neliö
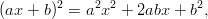
jonka termit ovat vakiota vaille annetun yhtälön kanssa. Tämän jälkeen lisätään ja vähennetään yhtälöön summan neliön vakio ja täydennetään neliöksi.
Esimerkiksi yhtälöä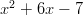 vastaava summan neliö on
vastaava summan neliö on
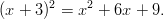
Lisätään ja vähennetään vakio alkuperäiseen yhtälöön, jolloin saadaan yhtälö täydennettyä neliöksi
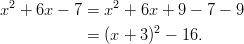
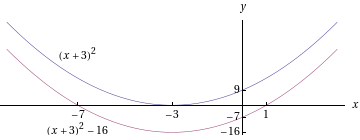
Neliöksi täydennetyn funktion kuvaajaa on yleensä helpompaa hahmotella, sillä kuvaaja on muuten samanlainen kuin summan neliön kuvaaja, kuvaajaa on vain siirretty vakion määräämään verran y-akselin suuntaisesti.
- Täydennetään neliöksi
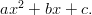
Etsitään sellainen summa, jonka neliö olisi vakioita vaille sama annetun polynomin kanssa. Summan ensimmäisen termin täytyy olla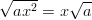 . Summan termien tulon täytyy olla
. Summan termien tulon täytyy olla 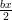 ja toiseksi
termiksi saadaan siis
ja toiseksi
termiksi saadaan siis 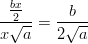 .
.
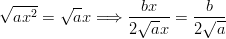
Nyt voidaan laskea summan jälkimmäisen termin neliö.
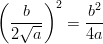
Nyt voidaan täydentää alkuperäinen polynomi neliöksi.
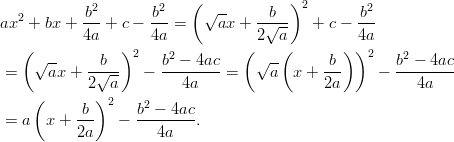
Vaihtoehtoisesti voidaan polynomista ottaa aluksi myös yhteiseksi tekijäksi kerroin
 , jolloin saadaan muokattavaksi yleensä helpompi
polynomi
, jolloin saadaan muokattavaksi yleensä helpompi
polynomi 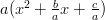 . Nyt sopiva summakin löydetään helposti,
sillä
. Nyt sopiva summakin löydetään helposti,
sillä
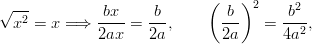
ja neliömuodoksi saadaan:
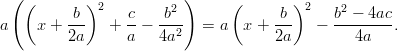
- Lasketaan
 , kun
, kun  ja
ja 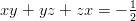 .
.
Ensin ratkaistaan jokin muuttuja ensimmäisen ehdon avulla, esimerkiksi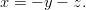
Sijoitetaan ratkaisu alkuperäiseen yhtälöön:
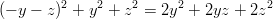
sekä jäljelle jäävään ehtoon:
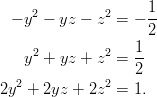
Sijoitetaan ehto yhtälöön:
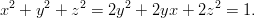
Siis
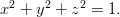
(LiveGr3D) Neljännen asteen polynomin kuvaaja
(Mma) Graph of a polynomial

Harjoitustehtäviä
- Jaa polynomit tekijöihin:
-
- Sievennä lausekkeet:
-
- Jaa polynomit tekijöihin:
-
- Täydennä polynomit neliöiksi:
-
Tehtävien vastaukset: