Lineaariset yhtälöt ja yhtälöryhmät

Lineaarinen yhtälö on yhtälö, joka on muotoa

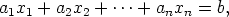
missä a₁,a₂,...,a_n ja b ovat vakioita ja symboleja x₁,x₂,...x_n sanotaan muuttujiksi. Lineaarisessa yhtälössä muuttujat ovat siis ensimmäistä astetta eli niiden potenssi on 1 (termi x² on toista astetta ja termi x³ kolmatta astetta ja niin edelleen). Luku a _i on muuttujan x_i kerroin. Yhtälön ratkaisu on vektori (c₁,c₂,...,c_n), joka toteuttaa yhtälön, toisin sanoen a₁c₁ + a₂c₂ + + a_nc_n = b.

Useasta lineaarisesta yhtälöstä muodostuu lineaarinen yhtälöryhmä

Lineaarisen yhtälöryhmän ratkaisu on vektori (c₁,c₂,...,c_n), joka toteuttaa yhtälöryhmän kaikki yhtälöt.

Lineaarinen yhtälöryhmä voidaan ratkaista koulukursseilla opitulla tavalla muuntamalla yhtälöryhmää ekvivalenttiin muotoon ja samalla siirtymällä kohti yhtälöryhmää, josta ratkaisut löydetään helposti. Tavallisia ekvivalentteja muunnoksia ovat yhtälön kertominen puolittain jollain nollasta eroavalla vakiolla ja yhtälön lisääminen puolittain toiseen yhtälöön.

Lineaarista yhtälöryhmää

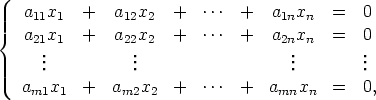
jossa kaikkien yhtälöiden oikeat puolet ovat nollia, sanotaan homogeeniseksi. Jokaisella homogeenisella yhtälöryhmällä on ainakin yksi ratkaisu nimittäin x₁ = x₂ = ... = x_n = 0. Tätä ratkaisua sanotaan triviaaliksi. Muita homogeenisen yhtälöryhmän ratkaisuja sanotaan epätriviaaleiksi.

Determinanttien teorian yhteydessä osoitetaan, että jos homogeenisessa yhtälöryhmässä on enemmän muuttujia kuin yhtälöitä (n > m), niin kyseisellä yhtälöryhmällä on aina epätriviaali ratkaisu.

Linkit:
Lineaarinen riippuvuus ja homogeeniset yhtälöryhmät