Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003 		LINEAARIALGEBRA
 

Determinantin perusominaisuuksien todistukset



     (D1)   Luku c on tekijänä jokaisessa summan sum sign(j1,j2,...,jn)a1j1...cakjk...anjn termissä, joten se voidaan ottaa koko summalausekkeen yhteiseksi tekijäksi.
     (D2)   Nyt determinantin summalauseke on
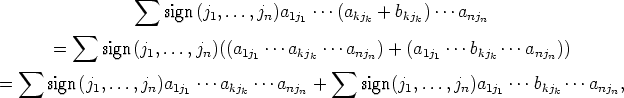sum sign(j1,...,jn)a1j ...(akj + bkj )...anj sum 1 k k n = sign(j1,...,jn)((a1j1 ...akjk ...anjn) + (a1j1 ...bkjk ...anjn)) sum sum = sign(j1,...,jn)a1j1 ...akjk ...anjn + sign(j1,...,jn)a1j1 ...bkjk ...anjn,
mistä väite seuraa.
     (D3)   Väite seuraa kohdasta (i), kun c = 0.
     (D4)   Todistetaan ensin, että väite pitää paikkansa, kun matriisissa A vaihdetaan kaksi peräkkäistä vaakariviä. Vaihdetaan vaakarivit Ai ja Ai+1, ja olkoon D muutetun matriisin determinantti. Nyt
sum D = sign(j ,...,j ,j ,...,j )a ...a a ...a . 1 i i+1 n 1,j1 i+1,jii,ji+1 n,jn

Koska sign(j1,...,ji,ji+1,...,jn) = -sign(j1,...,ji+1,ji,...,jn) ja koska tulossa tekijöiden järjestystä voidaan vaihtaa, saadaan

sum D= - sign(j1,...,ji+1,ji,...,jn)a1,j1 ...ai,ji+1ai+1,ji ...an,jn.

Tässä esiintyvä summa on sama kuin matriisin A determinantti, vain merkinnät ji ja ji+1 ovat vaihtaneet paikkaa keskenään. Täten on saatu ensimmäinen väite.

Todistetaan nyt alkuperäinen väite. Vaihdetaan matriisissa A i :s ja j :s, i < j, vaakarivi keskenään. Nyt i :s vaakarivi voidaan vaihtaa j :nneksi vaakariviksi j - i :llä peräkkäisten vaakarivien vaihdolla. Näiden vaihtojen jälkeen alkuperäinen j :s vaakarivi on järjestyksessä j - 1 :s vaakarivi. Se saadaan vaihdetuksi i :nneksi vaakariviksi j - i - 1 :llä peräkkäisten vaakarivien vaihdolla. Edellä todistetun mukaisesti matriisin, jossa i :s ja j :s vaakarivi on vaihdettu, determinantti on (-1)j-i-1+j-i det A = (-1)2(j-i)-1 det A = - det A.
     (D5)  Kun vaihdetaan matriisin kaksi samaa vaakariviä, matriisi ei muutu ja siten sen determinanttikaan ei voi muuttua. Toisaalta edellisen kohdan nojalla determinantti muuttuu vastaluvukseen. Täten determinantti on nolla.
     (D6)  Soveltamalla kohtia (D2) ja (D1) saadaan

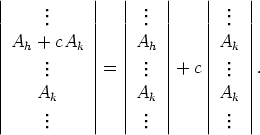
| | | | | | || ... || || ... || || ... || || A + cA || ||A || || A || | h . k | | .h | | k. | || .. ||= || .. ||+ c || .. ||. || Ak || ||Ak || || Ak || | . | | . | | . | | .. | | .. | | .. |

Kohdan (D5) perusteella yhtälön viimeinen determinantti on 0. Täten saadaan väite.

Linkit:
Determinantin perusominaisuuksia