Esimerkkejä ryhmistä

Esimerkki. Kokonaislukujen joukko muodostaa ryhmän, kun määritellään binäärioperaatioksi * yhteenlasku +. Tarkistetaan väite käymällä lävitse ehdot (G0) - (G3). Kokonaislukujen ominaisuuksien perusteella on selvää, että on suljettu operaation + suhteen ja että operaatio + on assosiatiivinen. Luku 0 on ryhmän (, +) neutraalialkio e, sillä kaikilla kokonaisluvuilla a :

Luvun a käänteisalkio a^-1 on nyt -a, sillä kaikilla a

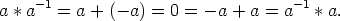
Nyt on näytetty, että (, +) on ryhmä. Koska a*b = a + b = b + a = b*a kaikilla a,b , niin todetaan vielä, että (, +) on Abelin ryhmä.

Samoin voidaan todeta, että (rationaaliluvut), (reaaliluvut) ja (kompleksiluvut) muodostavat Abelin ryhmät yhteenlaskun suhteen.

Esimerkki. Joukko ^* = \{0} on Abelin ryhmä kertolaskun  ^.  suhteen. Ehdot (G0), (G1) ja (G4) ovat selviä. Ryhmän (^*, ^. ) neutraalialkio on 1, sillä kaikilla a ^* :

Samoin todetaan, että alkion a ^* käänteisalkio on 1/a.

Samanlaisella päättelyllä voidaan osoittaa, että joukot \{0} ja \{0} ovat ryhmiä kertolaskun suhteen.

Esimerkki. Nopeasti ajateltuna voi tuntua, että kaikki joukot muodostavat ryhmiä luonnollisten operaatioiden suhteen. Näin ei kuitenkaan ole. Esimerkiksi joukko ei muodosta ryhmää kertolaskun suhteen. Ryhmän vaatimuksista toteutuvat kaikki ehdot paitsi (G3). Joukko on suljettu kertolaskun suhteen ja kertolasku on assosiatiivinen. Kaikilla luvuilla a käy neutraalialkioksi luku 1. Joukon alkiot ovat jopa kommutatiivisia kertolaskun suhteen. Ehdon (G3) toteutumiseksi pitäisi kaikilla alkioilla olla käänteisalkio. Luku 0 aiheuttaa hankaluuksia, sillä 0 ^. a = 0 kaikilla a , ja täten luvulla 0 ei ole käänteisalkiota. Käänteialkio on ongelmallinen muidenkin lukujen kuin 0 kanssa. Ehdosta a ^. a^-1 = 1 seuraa, että a^-1 = , mutta ei ole joukon alkio, kun a1. Siis muilla luvuilla kuin 1 ei ole käänteisalkiota.

Edellisen perusteella ei myöskään \{0} muodosta ryhmää kertolaskun suhteen.

Mieti, mikseivät , ja ole ryhmiä kertolaskun suhteen.

Linkit:
Ryhmä
Ryhmän perusominaisuuksia