Rengas

Rengas on algebrallinen systeemi, jossa on kaksi operaatiota. Tyypillinen esimerkki renkaasta on kokonaislukujen joukko varustettuna yhteen- ja kertolaskulla. Myös yleisessä määritelmässä on tapana käyttää operaatioina yhteen- ja kertolaskumerkintää. Kuten tavallista kertolaskun merkintä  ^.  jätetään usein merkitsemättä.

Määritelmä. Kolmikkoa (R, +, ^. ) sanotaan renkaaksi, jos se täyttää seuraavat ehdot:

     (R1)   (R, +) on Abelin ryhmä.
     (R2)   Jos a,b R, niin a ^. b R. Siis  ^.  on joukossa R määritelty binäärioperaatio.
     (R3)   Kaikilla a,b,c R on

     (R4)   Joukossa R on olemassa sellainen alkio 1_R, että kaikilla a R on a ^. 1 _R = 1_R ^. a = a. Alkiota 1_R sanotaan renkaan ykkösalkioksi.
     (R5)   Kaikilla a,b,c R on

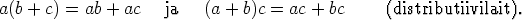
Jos operaatio  ^.  on lisäksi kommutatiivinen eli kaikilla a,b R on a ^. b = b ^. a, niin sanotaan, että (R, +, ^. ) on kommutatiivinen rengas.

Joskus renkaan määritelmästä jätetään postulaatti (R4) pois. Tällöin yllä määriteltyä rengasta sanotaan ykkösalkiolla varustetuksi.

Renkaan ykkösalkio 1_R on yksikäsitteinen. Nimittäin, jos renkaassa olisi kaksi ykkösalkiota 1_R ja 1_R ', niin postulaatin (R4) nojalla saadaan 1_R = 1_R' ^. 1 _R = 1_R'.

Postulaatin (R1) nojalla renkaassa on yhteenlaskun suhteen neutraalialkio e ja kaikkien alkioiden a vasta-alkiot -a. Renkaan tapauksessa neutraalialkiosta e puhutaan usein renkaan nolla-alkiona ja sitä merkitään 0_R. Lisäksi postulaatista (R1) seuraa, että yhteenlasku on assosiatiivinen ja kommutatiivinen.

Renkaasta (R, +, ^. ) voidaan puhua yksinkertaisesti vain renkaana R, jos operaatiot + ja  ^.  ovat asiayhteydestä selviä.

Linkit:
Ryhmä