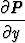Eksakti differentiaaliyhtälö

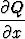Differentiaaliyhtälön (3x² + 6xy²) + (6x²y + 4y³)y' = 0 kerroinfunktioille P (x, y) = 3x² + 6xy² ja Q(x, y) = 6x²y + 4y³ pätee

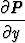= 12xy = ,

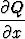ja yhtälö on siis eksakti.

Tällöin sillä on muotoa F (x, y) = C oleva ratkaisu, missä

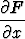= P (x, y) = 3x² + 6xy²  ja  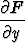 = Q(x, y) = 6x²y + 4y³.

Eksakti yhtälö ratkaistaan integroimalla aluksi jompikumpi näistä yhtälöistä. Jos edellinen integroidaan muuttujan x suhteen, saadaan

F (x, y) = x³ + 3x²y² + f(y).

Tässä oleva integroimisvakio f(y) voi riippua muuttujasta y.

Funktio f(y) saadaan määritetyksi jälkimmäisen ehdon perusteella:

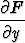= Q(x, y)  eli  6x²y + f'(y) = 6x²y + 4y³,

jolloin f' (y) = 4y³ ja siis f(y) = y⁴.

Differentiaaliyhtälön yleinen ratkaisu on tällöin

x³ + 3x²y² + y⁴ = C.

Funktion f lausekkeessa voisi periaatteessa esiintyä myös integroimisvakio, mutta tämä on merkityksetön, koska sen voidaan katsoa sisältyvän yleisen ratkaisun vakioon C.