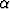 -,
-, 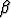 - tai
- tai 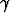 -säteilyn kautta. Hiukkassäteilyn eli
-säteilyn kautta. Hiukkassäteilyn eli 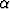 - ja
- ja 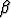 -säteilyn tapauksessa samalla muuttuu myös atomiytimen sisäinen kokoonpano. Tällaisen hajoamisen kautta alkuaine muuttuu toiseksi.
-säteilyn tapauksessa samalla muuttuu myös atomiytimen sisäinen kokoonpano. Tällaisen hajoamisen kautta alkuaine muuttuu toiseksi.
| radahaj2.nb |
Radioaktiivinen hajoaminen on ilmiö, jossa aktivoitunut, epästabiili atomiydin vapauttaa energiaansa 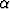 -,
-, 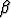 - tai
- tai 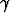 -säteilyn kautta. Hiukkassäteilyn eli
-säteilyn kautta. Hiukkassäteilyn eli 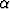 - ja
- ja 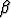 -säteilyn tapauksessa samalla muuttuu myös atomiytimen sisäinen kokoonpano. Tällaisen hajoamisen kautta alkuaine muuttuu toiseksi.
-säteilyn tapauksessa samalla muuttuu myös atomiytimen sisäinen kokoonpano. Tällaisen hajoamisen kautta alkuaine muuttuu toiseksi.
Erityisen paljon tutkittuja ovat ydinreaktorien polttoainesauvoihin jäävien radiokatiivisten aineiden hajoamisketjut. Polttoainesauvoista muodostuva pitkään radioaktiivinen jäte aiheuttaa huolestumista, koska sauvoissa olevien radioaktiivisten aineiden hajoaminen on niin hidasta, että säteilyongelma säilyy luonnollisen hajoamisen kautta akuuttina vuosituhansia. Tämä esimerkki käsittelee radiumin ![[Graphics:Images/radahaj2_gr_1.gif]](Images/radahaj2_gr_1.gif) hajoamista sekä yksinkertaistettua radiumin
hajoamista sekä yksinkertaistettua radiumin ![[Graphics:Images/radahaj2_gr_2.gif]](Images/radahaj2_gr_2.gif) ytimen hajoamisketjua lyijyksi
ytimen hajoamisketjua lyijyksi ![[Graphics:Images/radahaj2_gr_3.gif]](Images/radahaj2_gr_3.gif) . Tämä ketju muodostaa loppuosan varsin tärkeästä toriumin
. Tämä ketju muodostaa loppuosan varsin tärkeästä toriumin ![[Graphics:Images/radahaj2_gr_4.gif]](Images/radahaj2_gr_4.gif) hajoamisketjusta.
hajoamisketjusta.
Jokaiselle radioaktiiviselle atomiytimelle on olemassa tietty todennäköisyys sen hajoamiseen määrätyllä aikavälillä. Hajoamisen kautta syntyvien tytäratomien lukumäärä on siten suoraan verrannollinen aktiivisten atomiytimien lukumäärään. Niinpä voidaan määrittää radioaktiivinen hajoamislaki
![[Graphics:Images/radahaj2_gr_5.gif]](Images/radahaj2_gr_5.gif)
missä ![[Graphics:Images/radahaj2_gr_6.gif]](Images/radahaj2_gr_6.gif) on radioaktiivisten ytimien lukumäärä,
on radioaktiivisten ytimien lukumäärä, ![[Graphics:Images/radahaj2_gr_7.gif]](Images/radahaj2_gr_7.gif)
![[Graphics:Images/radahaj2_gr_8.gif]](Images/radahaj2_gr_8.gif) radioaktiivinen hajoamisvakio, joka määrittää todennäköisyyden atomiytimen spontaanille hajoamiselle annetulla ajanhetkellä. Hajoamislain perusteella voidaan määrittää ns. puoliintumisaika
radioaktiivinen hajoamisvakio, joka määrittää todennäköisyyden atomiytimen spontaanille hajoamiselle annetulla ajanhetkellä. Hajoamislain perusteella voidaan määrittää ns. puoliintumisaika ![[Graphics:Images/radahaj2_gr_9.gif]](Images/radahaj2_gr_9.gif) , joka ilmoittaa sen aikayksikön, jossa puolet alkuperäisistä ytimistä on hajonnut. Integroimalla saadaan hajoamattomien ytimien lukumäärälle
, joka ilmoittaa sen aikayksikön, jossa puolet alkuperäisistä ytimistä on hajonnut. Integroimalla saadaan hajoamattomien ytimien lukumäärälle
![[Graphics:Images/radahaj2_gr_10.gif]](Images/radahaj2_gr_10.gif)
jossa ![[Graphics:Images/radahaj2_gr_11.gif]](Images/radahaj2_gr_11.gif) on ydinten lukumäärä ajanhetkellä
on ydinten lukumäärä ajanhetkellä ![[Graphics:Images/radahaj2_gr_12.gif]](Images/radahaj2_gr_12.gif)
![[Graphics:Images/radahaj2_gr_13.gif]](Images/radahaj2_gr_13.gif) saadaan puoliintumisajalle
saadaan puoliintumisajalle ![[Graphics:Images/radahaj2_gr_14.gif]](Images/radahaj2_gr_14.gif) . Tällöin hajoamislaille pätee
. Tällöin hajoamislaille pätee
![[Graphics:Images/radahaj2_gr_15.gif]](Images/radahaj2_gr_15.gif)
Radium ![[Graphics:Images/radahaj2_gr_16.gif]](Images/radahaj2_gr_16.gif) on yksi väliydin pitkäaktiivisen
on yksi väliydin pitkäaktiivisen ![[Graphics:Images/radahaj2_gr_17.gif]](Images/radahaj2_gr_17.gif) :n hajoamisketjussa.
:n hajoamisketjussa. ![[Graphics:Images/radahaj2_gr_18.gif]](Images/radahaj2_gr_18.gif) :n puoliintumisaika on 5,75 vuotta sen hajotessa lyhytaktiiviseksi
:n puoliintumisaika on 5,75 vuotta sen hajotessa lyhytaktiiviseksi ![[Graphics:Images/radahaj2_gr_19.gif]](Images/radahaj2_gr_19.gif) -ytimeksi. Lasketaan kuinka paljon 100 kg:sta
-ytimeksi. Lasketaan kuinka paljon 100 kg:sta ![[Graphics:Images/radahaj2_gr_20.gif]](Images/radahaj2_gr_20.gif) :sta on jäljellä 70 vuoden kuluttua.
:sta on jäljellä 70 vuoden kuluttua.
Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.
![[Graphics:Images/radahaj2_gr_21.gif]](Images/radahaj2_gr_21.gif)
Ytimien hajoamista kuvaava differentiaaliyhtälö.
![[Graphics:Images/radahaj2_gr_22.gif]](Images/radahaj2_gr_22.gif)
Alkuehdon määrittää tilanne, jossa on vain ![[Graphics:Images/radahaj2_gr_24.gif]](Images/radahaj2_gr_24.gif) ytimiä. Lasketaan ainemäärä kilogrammoissa.
ytimiä. Lasketaan ainemäärä kilogrammoissa.
![[Graphics:Images/radahaj2_gr_25.gif]](Images/radahaj2_gr_25.gif)
Ratkaistaan differentiaaliyhtälö.
![[Graphics:Images/radahaj2_gr_27.gif]](Images/radahaj2_gr_27.gif)
Sievennetään tulos ja sijoitetaan siihen hajoamisvakio. Käytetään aikayksikkönä vuosia.
![[Graphics:Images/radahaj2_gr_29.gif]](Images/radahaj2_gr_29.gif)
Piirretään kuvaaja ainemäärän kehitykselle ajan fuktiona 50 vuoden aikajaksolla.
![[Graphics:Images/radahaj2_gr_31.gif]](Images/radahaj2_gr_31.gif)
![[Graphics:Images/radahaj2_gr_32.gif]](Images/radahaj2_gr_32.gif)
70 vuoden jälkeen jäljelle jääneen ainemäärän paino kilogrammoissa selviää sijoittamalla ajaksi 70 vuotta.
![[Graphics:Images/radahaj2_gr_34.gif]](Images/radahaj2_gr_34.gif)
Tuloksena on siis 21,6 grammaa Radium ![[Graphics:Images/radahaj2_gr_36.gif]](Images/radahaj2_gr_36.gif) :aa.
:aa.
Myös Radium ![[Graphics:Images/radahaj2_gr_37.gif]](Images/radahaj2_gr_37.gif) on väliydin
on väliydin ![[Graphics:Images/radahaj2_gr_38.gif]](Images/radahaj2_gr_38.gif) :n hajoamisketjussa. Hajoamisketju
:n hajoamisketjussa. Hajoamisketju ![[Graphics:Images/radahaj2_gr_39.gif]](Images/radahaj2_gr_39.gif) ytimestä eteenpäin sisältää useita lyhytaikaisia ja muutamia pitkäaikaisia väliytimiä ennen hajoamista pysyväksi lyijy-ytimeksi
ytimestä eteenpäin sisältää useita lyhytaikaisia ja muutamia pitkäaikaisia väliytimiä ennen hajoamista pysyväksi lyijy-ytimeksi ![[Graphics:Images/radahaj2_gr_40.gif]](Images/radahaj2_gr_40.gif) . Tarkastelemme nyt hajoamista väliytimet
. Tarkastelemme nyt hajoamista väliytimet ![[Graphics:Images/radahaj2_gr_41.gif]](Images/radahaj2_gr_41.gif) ja
ja ![[Graphics:Images/radahaj2_gr_42.gif]](Images/radahaj2_gr_42.gif) huomioiden. Puoliintumisajat ytimien hajoamisille ovat seuraavat:
huomioiden. Puoliintumisajat ytimien hajoamisille ovat seuraavat:
![[Graphics:Images/radahaj2_gr_43.gif]](Images/radahaj2_gr_43.gif)
![[Graphics:Images/radahaj2_gr_44.gif]](Images/radahaj2_gr_44.gif)
Muodostetaan hajoamisketjua kuvaavat differentiaaliyhtälöt:
![[Graphics:Images/radahaj2_gr_45.gif]](Images/radahaj2_gr_45.gif)
jossa ![[Graphics:Images/radahaj2_gr_46.gif]](Images/radahaj2_gr_46.gif) on
on ![[Graphics:Images/radahaj2_gr_47.gif]](Images/radahaj2_gr_47.gif) -atomien lukumäärä ja
-atomien lukumäärä ja ![[Graphics:Images/radahaj2_gr_48.gif]](Images/radahaj2_gr_48.gif) vastaavasti
vastaavasti ![[Graphics:Images/radahaj2_gr_49.gif]](Images/radahaj2_gr_49.gif) :n hajoamisvakio. Vastaavasti alaindeksi '2' viittaa
:n hajoamisvakio. Vastaavasti alaindeksi '2' viittaa ![[Graphics:Images/radahaj2_gr_50.gif]](Images/radahaj2_gr_50.gif) :n, '3'
:n, '3' ![[Graphics:Images/radahaj2_gr_51.gif]](Images/radahaj2_gr_51.gif) :n ja '4'
:n ja '4' ![[Graphics:Images/radahaj2_gr_52.gif]](Images/radahaj2_gr_52.gif) :n vastaaviin suureisiin. Ratkaistaan hajoamisketjun differentiaaliyhtälöryhmä ja piirretään kuvaajat ytimien lukumäärille ajan funktioina.
:n vastaaviin suureisiin. Ratkaistaan hajoamisketjun differentiaaliyhtälöryhmä ja piirretään kuvaajat ytimien lukumäärille ajan funktioina.
Ytimien hajoamisia ja toisikseen muuttumista kuvaa seuraava normaaliryhmä.
![[Graphics:Images/radahaj2_gr_53.gif]](Images/radahaj2_gr_53.gif)
Ongelman tuntemattomat funktiot ovat ketjun eri alkuaineiden ydinten lukumäärät.
![[Graphics:Images/radahaj2_gr_55.gif]](Images/radahaj2_gr_55.gif)
Alkuehdon määrittää tilanne, jossa on ![[Graphics:Images/radahaj2_gr_57.gif]](Images/radahaj2_gr_57.gif) kpl
kpl ![[Graphics:Images/radahaj2_gr_58.gif]](Images/radahaj2_gr_58.gif) ytimiä (n. 3,72
ytimiä (n. 3,72![[Graphics:Images/radahaj2_gr_59.gif]](Images/radahaj2_gr_59.gif) g):
g):
![[Graphics:Images/radahaj2_gr_60.gif]](Images/radahaj2_gr_60.gif)
Hajoamisvakiot ovat
![[Graphics:Images/radahaj2_gr_62.gif]](Images/radahaj2_gr_62.gif)
Ratkaistaan differentiaaliyhtälöryhmä ja sievennetään tulokset:
![[Graphics:Images/radahaj2_gr_66.gif]](Images/radahaj2_gr_66.gif)
![[Graphics:Images/radahaj2_gr_68.gif]](Images/radahaj2_gr_68.gif)
![[Graphics:Images/radahaj2_gr_69.gif]](Images/radahaj2_gr_69.gif)
|
![[Graphics:Images/radahaj2_gr_70.gif]](Images/radahaj2_gr_70.gif)
|
![[Graphics:Images/radahaj2_gr_71.gif]](Images/radahaj2_gr_71.gif)
|
![[Graphics:Images/radahaj2_gr_72.gif]](Images/radahaj2_gr_72.gif)
|
Piirretään kuva ainemäärien muuttumisesta ajan funktiona. Tarkasteltavana aikavälinä käytetään yhtä kuukautta.
![[Graphics:Images/radahaj2_gr_73.gif]](Images/radahaj2_gr_73.gif)
![[Graphics:Images/radahaj2_gr_74.gif]](Images/radahaj2_gr_74.gif)
![[Graphics:Images/radahaj2_gr_75.gif]](Images/radahaj2_gr_75.gif)
Lähtöytimien ![[Graphics:Images/radahaj2_gr_77.gif]](Images/radahaj2_gr_77.gif) (vihreä) hajoamisessa syntyy ensin turkoosilla merkittyjä
(vihreä) hajoamisessa syntyy ensin turkoosilla merkittyjä ![[Graphics:Images/radahaj2_gr_78.gif]](Images/radahaj2_gr_78.gif) ytimiä jotka nopeasti hajoavat violetilla merkityiksi
ytimiä jotka nopeasti hajoavat violetilla merkityiksi ![[Graphics:Images/radahaj2_gr_79.gif]](Images/radahaj2_gr_79.gif) ytimiksi. Niiden puoliintumisaika on kuitenkin niin lyhyt, että ne hajoavat hyvin nopeasti
ytimiksi. Niiden puoliintumisaika on kuitenkin niin lyhyt, että ne hajoavat hyvin nopeasti ![[Graphics:Images/radahaj2_gr_80.gif]](Images/radahaj2_gr_80.gif) ytimiksi. Jo viidentoista päivän kuluttua lähtöhetkestä on jäljellä lähinnä vain vakaita punaisella piirrettyjä
ytimiksi. Jo viidentoista päivän kuluttua lähtöhetkestä on jäljellä lähinnä vain vakaita punaisella piirrettyjä ![[Graphics:Images/radahaj2_gr_81.gif]](Images/radahaj2_gr_81.gif) ytimiä. Eniten niiden syntymistä hidastaa lähtöytimien verrattain lyhyt puoliintumisaika.
ytimiä. Eniten niiden syntymistä hidastaa lähtöytimien verrattain lyhyt puoliintumisaika.
Testaa puoliintumisajan vaikutusta radioaktiivisessa hajoamisessa. Mikäli puolitat ![[Graphics:Images/radahaj2_gr_82.gif]](Images/radahaj2_gr_82.gif) :n puoliintumisajan, kuinka paljon vähemmän ytimiä on jäljellä 4 puoliintumisajan jälkeen verrattuna todelliseen tilanteeseen?
:n puoliintumisajan, kuinka paljon vähemmän ytimiä on jäljellä 4 puoliintumisajan jälkeen verrattuna todelliseen tilanteeseen?
Mikäli haluat tutustua tarkemmin radioaktiivisiin hajoamisketjuihin, voit tutustua niihin Internetissä Uranium Information Centren kotisivuilla Australiassa. Loistava laskuri hajoamisketjujen simuloimiseksi löytyy Project Javan kotisivuilta, missä yksi ohjelmointikilpailutyö keskittyy hajoamisketjujen laskemiseen.