Tykillä ampuminen 2

Mallinnettaessa heittoliikettä, kuten esimerkiksi tykillä ampumista, keskeisinä vaikuttavina tekijöinä ovat painovoima sekä ilmanvastuksen aiheuttama nopeudelle vastakkaissuuntainen voima.

Painovoima on, missä on maan vetovoiman aiheuttama kiihtyvyys ja heitettävän kappaleen massa. Ilmanvastusvoima on verrannollinen nopeuden neliöön, ja se voidaan mallintaa lausekkeella

missä on ilmanvastuskerroin, skalaarinen nopeus, nopeus vektorina ja nopeuden suuntainen yksikkövektori.

Yleinen liikeyhtälö saa tällöin muodon

missä on merkitty sekä .

Tarkastellaan tilannetta, jossa tykillä ammutaan poispäin liikkuvaan maaliin. Mikä on oikea ampumiskulma, kun 25 metrin korkeudella sijaitsevalta tykkilavetilta ammutaan 10 kg kranaatti nopeudella 1000 m/s kohti maalia, jonka etäisyys ampumishetkellä on tasan 5 km? Maali liikkuu 15 m/s tykistä poispäin veden pintaa pitkin, ja ilmanvastuskerroin kranaatille on .

Jaetaan yllä esitetty toisen kertaluvun vektorimuotoinen differentiaaliyhtälö kahteen eri osayhtälöön, z-suuntaan ja x-suuntaan, ja ratkaistaan yhtälöt. Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.

Määritellään differentiaaliyhtälöryhmä  ja sen tuntemattomat muuttujat.

Määritellään vakiot ja alkuehto. Ammuksen lähtökulma olkoon . Sisällytetään ehtoon sekä ammuksen alkunopeus jaettuna nopeuskomponentteihin että lähtökorkeus.

Differentiaaliyhtälöryhmä ei ole ratkaistavissa alkeisfunktioiden avulla, joten ryhmää ei voi ratkaista Mathematican avulla 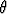:n funktiona. Suljetussa muodossa olevan ratkaisun sijaan joudutaan turvautumaan arvaukseen. Arvataan jokin kulma (radiaaneissa), ja katsotaan, miten hyvin laukaus osui.

Muokataan tulos käyttökelpoiseen muotoon ja piirretään kuvio.

Katsotaan miten lähelle laukaus osui. Huomaa, että ratkaisussa on huomioitu myös kohteen liike.

Ammus osuu veteen noin puolitoista kilometriä liian kauaksi. Lähtökulma oli siis liian suuri. Arvataan uudestaan tarkoituksena haarukoida oikea tulos arvausten väliin. Tämän jälkeen voidaan systemaattisesti hakea oikea kulma.

Nyt laukaus jäi liian lyhyeksi. Oikea lähtökulma on kuitenkin saatu haarukoiduksi. Tarkan ampumiskulman löytämiseksi tehdään organisoitu kokeilu, johon otetaan aluksi 21 laskupistettä 0.001 radiaanin välein.

Lasketaan kulma ja sen avulla lasketut yhtälöt omaan taulukkoonsa ja osumaetäisyydet omaansa.

Etsitään lähintä osumaa vastaava indeksi ja tämän avulla ampumiskulma ja osumaetäisyys.

Sama uudestaan uudella kapeammalla haarukalla ja 0.0001 radiaanin askelvälillä.

Osuma on siis runsaan kuuden metrin päässä ja vastaava ampumiskulma on asteissa

Tehtäviä

Piirrä lähimmäksi osuvan ammuksen lentorata. Määritä radan lakikorkeus ja ammuksen lentoaika.

Suurenna ilmanvastuskerrointa, ja tutki, miten se vaikuttaa radan muotoon.