Epälineaarisuus ja kaaos

Epälineaariset differentiaaliyhtälöt ovat yksinkertaisesti differentiaaliyhtälöitä, jotka eivät ole lineaarisia. Niiden ratkaisuissa esiintyy usein piirteitä, joita lineaaristen yhtälöiden ratkaisuilla ei ole.

Alkuarvoprobleeman ratkaisua kutsutaan stabiiliksi, jos — hieman epätäsmällisesti ilmaisten — lähellä toisiaan olevia alkuehtoja vastaavat ratkaisut myös ovat lähellä toisiaan. Lineaarisen yhtälönkin ratkaisut voivat olla epästabiileja. Esimerkiksi yhtälön y' = y alkuehtoja y(0) = 1 ja y(0) = 1.01 vastaavat ratkaisut ovat y₁ = e^x ja y₂ = 1.01e^x. Näiden erotus y₂ - y₁ = 0.01e^x kasvaa rajatta, kun x , ts. ratkaisut eivät ainakaan koko alueessa x > 0 pysy lähellä toisiaan. Periatteessa niiden käyttäytyminen on kuitenkin samantyyppistä. Selkeämpi ero tulee esiin verrattaessa alkuehtoja y(0) = 0.01 ja y(0) = -0.01 vastaavia ratkaisuja.

Epälineaarisilla yhtälöillä saattaa esiintyä epästabiileja ilmiöitä, joita on tullut tavaksi kutsua kaoottiseksi käyttäytymiseksi. Kaikilla epälineaarisila yhtälöillä näitä ei kuitenkaan ole. Hyvä esimerkki kaoottisuudesta on toisiinsa kytkettyjä heilureita kuvaava yhtälöryhmä

Oheiset kuvat esittävät alkuehtoja y(0) = z(0) = 0, y'(0) = 2.1, z'(0) = 2 ja y(0) = z(0) = 0, y'(0) = 2.101, z'(0) = 2 vastaavia ratkaisuja yz-tasossa. Ratkaisut poikkeavat merkittävästi toisistaan, vaikka alkuehtojen välinen ero on hyvin vähäinen.

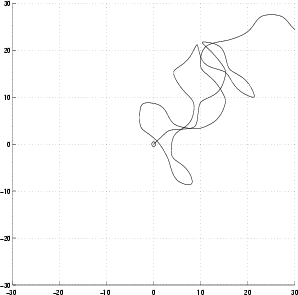
Kuvatunkaltainen epästabiilisuus merkitsee, että ratkaisujen numeerinen laskeminen tulee lähes mahdottomaksi: mitätön ero alkuarvoissa tai mitätön pyöristysvirhe numeerisessa laskennassa voi johtaa täysin toisenlaiseen ratkaisukäyrään. Itse asiassa edellä oleviin kuviinkaan ei ole luottamista: ne on laskettu numeerisesti.

Monien luonnonilmiöiden kehittymistä ajan mukana — esimerkkinä vaikkapa sääilmiöt ilmakehässä — kuvataan differentiaaliyhtälöillä. Jos yhtälöiden ratkaisut käyttäytyvät kaoottisesti, ei differentiaaliyhtälömallista periaatteessakaan voida saada kovin hyvin tietoa ilmiöiden kehittymisestä, vaikka malli sinänsä olisikin deterministinen, ts. annettuun alkuehtoon liittyisi yksikäsitteinen ratkaisu. Alkuarvot saadaan nimittäin havainnoista — ilmakehän tapauksessa lämpötila, ilmanpaine, tuulen suunta jne. eri havaintopaikoilla — ja näiden tarkkuus on aina rajallinen. Jos ratkaisut käyttäytyvät kaoottisesti, voi mittausvirhe vaikuttaa oleellisesti mallin antamaan ratkaisuun.