Kvalitatiivinen näkökulma

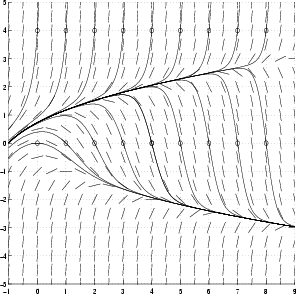
Ensimmäisen kertaluvun differentiaaliyhtälön y' = f(x, y) suuntakenttä xy-tasossa tai toisen kertaluvun autonomisen yhtälön suuntakenttä faasitasossa antavat mahdollisuuden tarkastella ratkaisujen kvalitatiivisia ominaisuuksia ilman, että yhtälöä on tarpeen ratkaista. Vastaavanlaisia ilmiöitä esiintyy korkeampien kertalukujen yhtälöillä, mutta graafinen tarkastelu ei ole yhtä yksinkertaista.

Alla oleva vasemmanpuoleinen kuvio esittää eräitä yhtälön y' = y² - x ratkaisukäyriä suuntakenttään piirrettyinä. Kuvioon hahmottuu kaksi erikoisasemassa olevaa ratkaisukäyrää:

Ylemmästä pyrkivät kaikki muut ratkaisukäyrät loitontumaan, kun x kasvaa (ts. siirrytään vasemmalta oikealle). Jos käyrän päälle asetetaan kapea nauha, kaikki muut ratkaisut siirtyvät tämän nauhan ulkopuolelle ennemmin tai myöhemmin. Poikkeuksena on yksi ratkaisu: kyseinen käyrä itse.

Alempana on vastaavasti käyrä, jota kaikki ylemmän käyrän alapuolella olevat yhtälön ratkaisut asymptoottisesti lähestyvät, kun x . Jos tämän käyrän päälle asetetaan miten kapea nauha tahansa, muut ratkaisut siirtyvät sen alle ennemmin tai myöhemmin.

Oikeanpuoleinen kuvio esittää van der Polin differentiaaliyhtälön y'' - (1 - y²)y' + y = 0 ratkaisuja faasitasossa (vaaka-akselilla y, pystyakselilla y'). Kaikki ratkaisut (lukuunottamatta tapausta y(x) = 0 kaikilla x) lähestyvät tiettyä umpinaista käyrää, kun x .