| k1 | = hf(xk, yk), | ||
| k2 | = hf(xk + h/2, yk + k1/2), | ||
| k3 | = hf(xk + h/2, yk + k2/2), | ||
| k4 | = hf(xk + h, yk + k3), | ||
| yk+1 | = yk +  (k1 + 2k2 + 2k3 + k4). |
Samaan tapaan kuin parannetun Eulerin menetelmän johtamisessa käytetään toisen asteen Taylorin polynomia, voidaan tarkastella neljännen asteen polynomia. Tarkasteluista tulee tällöin suhteellisen monimutkaisia, mutta tuloksena saadaan klassinen Rungen – Kuttan menetelmä, joka voidaan luonnehtia useampikertaiseksi ennustaja-korjaaja-menetelmäksi.
Yhden askelen laskemisessa tarvittavat kaavat ovat seuraavat:
| k1 | = hf(xk, yk), | ||
| k2 | = hf(xk + h/2, yk + k1/2), | ||
| k3 | = hf(xk + h/2, yk + k2/2), | ||
| k4 | = hf(xk + h, yk + k3), | ||
| yk+1 | = yk + (k1 + 2k2 + 2k3 + k4). |
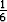(k1 + 2k2 + 2k3 + k4)
mieltää funktion f eräissä pisteissä laskettujen arvojen painotetuksi keskiarvoksi
kerrottuna tarkasteluvälin pituudella h. Se voi siis hyvin olla järkevä approksimaatio
integraalille
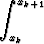f(x, y(x)) dx.
Klassinen Rungen – Kuttan menetelmä on varsin hyvä ja melko laajasti käytetty menetelmä alkuarvoprobleemojen ratkaisemisessa. Vastaavantyyppisiä yhteisellä nimellä Rungen – Kuttan menetelmiksi kutsuttuja menetelmiä on useita erilaisia.