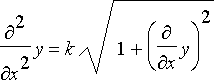Sovellukset : Geometrinen fysiikka

Roikkuva ketju

Tarkastellaan kitkattoman, taipuisan ketjun potentiaalienergiaa. Jos ketju riippuu molemmista päistä kiinnitettynä, se hakee muodon, joka antaa potentiaalienergialle minimiarvon. Variaatiolaskennan avulla voidaan osoittaa, että kun ketjun potentiaalienergialla on minimi, niin ketjun muoto y = y ( x ) noudattaa differentiaaliyhtälöä

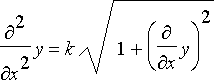diff(y,`$`(x,2)) = k*sqrt(1+diff(y,x)^2) .

Tässä k on ketjun pituuden epäsuorasti määräävä tekijä. Tarkastellaan roikkuvan ketjun muotoa eri reunaehdoilla. Poistetaan ensin vanhat muuttujat.

> restart;

Muodostetaan ketjua kuvaava toisen kertaluvun differentiaaliyhtälö. Valitaan k = 1.

> k:= 1:
yht:= diff(y(x), x$2)=k*sqrt(1+diff(y(x), x)^2);

yht := diff(y(x),`$`(x,2)) = sqrt(1+diff(y(x),x)^2)...

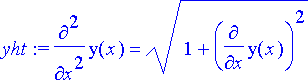
Valitaan reunaehdot symmetrisesti origon molemmin puolin. Ketju olkoon kiinnitetty pisteissä x = 1 ja x = -1.

> reunaehto1:= y(-1)=0, y(1)=0;

reunaehto1 := y(-1) = 0, y(1) = 0

Ratkaistaan yhtälö

> rtk:= dsolve({yht, reunaehto1}, y(x));

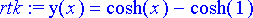
rtk := y(x) = cosh(x)-cosh(1)

Ketjun muoto noudattaa hyperbolista kosinia, jonka kuvaajaa tästä syystä kutsutaankin ketjukäyräksi .

Piirretään kuvaaja ketjun riippumisasennolle.

> kaari:= rhs(rtk);

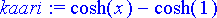
kaari := cosh(x)-cosh(1)

> plot(kaari, x=-1..1, scaling=constrained);

[Maple Plot]

Entä kun ketjun toinen pää on merkittävästi korkeammalla? Muutetaan reunaehtoja ja ratkaistaan yhtälöt.

> reunaehto2:= y(-1)=0, y(1)=3;

reunaehto2 := y(-1) = 0, y(1) = 3

> rtk2:= dsolve({yht, reunaehto2}, y(x));

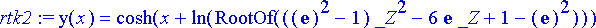
rtk2 := y(x) = cosh(x+ln(RootOf((exp(1)^2-1)*_Z^2-6...

Maple palauttaa ratkaisun RootOf muodossa, joka edustaa yleisesti jotakin yhtälön juurta. Loppuun asti lasketut ratkaisut saadaan komennolla allvalues .

> kaari2:= allvalues(rtk2):
evalf(%);

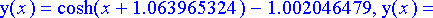
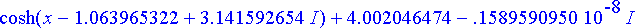
y(x) = cosh(x+1.063965324)-1.002046479, y(x) = cosh...

Tulokseksi saadaan hieman monimutkaisempi riippumiskäyrä. Valitaan ylöspäin aukeava ratkaisu (cosh( x + c )) ja piirretään sen kuvaaja.

> plot(rhs(kaari2[1]), x=-1..1);

[Maple Plot]

Kun käyrän yhtälö ilmaistaan muodossa y = f ( x ), saadaan käyrän pituus L laskemalla

L = int(sqrt(1+diff(y,x)^2),x = x[1] .. x[2]) .

Tätä yhtälöä voidaan soveltaa myös ratkaistuihin riippuvien ketjujen yhtälöihin. Lasketaan ensimmäisenä lasketun käyrän pituus. Määritellään ensin integraalin sisällä oleva funktio.

> fkt:= sqrt(1+diff(kaari, x)^2);

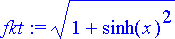
fkt := sqrt(1+sinh(x)^2)

Sitten integroidaan.

> pit:= int(fkt, x=-1..1):
evalf(%);

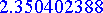
2.350402388

Tehtäviä

Portaikko suljetaan ketjulla, joka ripustetaan kahden tolpan välille. Tolppien etäisyys on 1 m ja korkeus 70 cm. Ratkaise graafisesti kokeilemalla ( k :n arvoa muuttamalla), minkä pituinen ketju tarvitaan, kun ketjun alimmaiskorkeuden tulee olla vähintään 50 cm. Kun muutat k :n arvoa, saatat kohdata yllättäviä vaikeuksia differentiaaliyhtälön ratkaisussa. Ketjun pituudeksi tulee n. 109.7 cm.

Roikkuvan ketjun potentiaalienergiaa kuvaa integraali

int(y(x)*sqrt(1+diff(y(x),x)^2),x = x[1] .. x[2]) ,

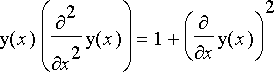kun ketjun massatiheys pituusyksikköä kohden on asetettu = 1. Variaatiolaskennan Eulerin yhtälön mukaan tämä saa minimiarvonsa, kun y(x)*diff(y(x),`$`(x,2)) = 1+diff(y(x),x)^2 . Etsi tämän yhtälön yleinen ratkaisu alkeisfunktioiden avulla. Johda edellä lähtökohdaksi otettu differentiaaliyhtälö ratkaisun avulla. Vihje: Kyseessä on toisen kertaluvun yhtälö, jossa muuttuja x ei esiinny eksplisiittisesti.

Teoria: reunaehto
Ratkaiseminen: muotoa

JP & SKK & MS 12.07.2001