Parabolinen peili

Taskulamppu on kaikille tuttu arkinen kapistus. Hyvän taskulampun valo tulee yhdensuuntaisena keilana ulos valaisimesta eikä hajavaloa juuri synny. Tällaisella valaisimella voidaan valaista kaukanakin oleviin kohteisiin hyvällä valovoimalla. Jotta lampulla olisi nämä ominaisuudet, siinä olevan heijastinpeilin tulee heijastaa mihin tahansa suuntaan polttimosta lähtevä valo samansuuntaisena säteenä ulos valaisimesta. Tällaisen peilipinnan idea on esitetty alla olevassa kuvassa.

Selvitetään kyseisen peilinkaaren muoto. Kuvasta voimme nähdä, että mikäli lamppu sijaitsee origossa,

= .

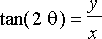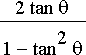Lisäksi kuvaajan geometria paljastaa, että käyrän tangentin suuntakulma pisteessä ( x , y ) on 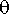eli

.

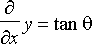Sijoittamalla saadaan

.

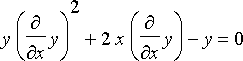Ratkaisemalla tämä yhtälö voidaan ratkaista peilin muoto xy-koordinaatistossa, kun lampun polttimo sijaitsee origossa.

Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.

> restart;

Muodostetaan differentiaaliyhtälö.

> yht:= y(x)*diff(y(x), x)^2+2*x*diff(y(x), x)-y(x)=0;

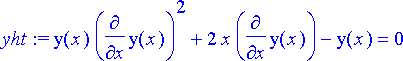
Valitaan alkuehdoksi käyrän ja x-akselin leikkauspiste. Se olkoon kohdassa x = -1.

> alkuehto:= y(-1)=0;

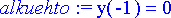
Ratkaistaan differentiaaliyhtälöryhmä. Probleeman tuntematon funktio on y( x ).

> rtk:= dsolve({yht, alkuehto}, y(x));

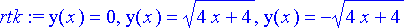
Differentiaaliyhtälöllä on selvästikin ratkaisuna nollafunktio, mutta tämä ei ole probleeman kannalta mielenkiintoinen.

Erilaiset ratkaisut antavat peilin ylä- ja alaosan muodon. Piirretään kuva.

> with(plots): with(plottools):

Warning, the name changecoords has been redefined

> display(plot([rhs(rtk[3]), rhs(rtk[2])], x=-1..5, color=blue), circle([0,0], 0.3, color=red, thickness=3), disk([0,0], 0.3, color=yellow), scaling=constrained);

Peili on muodoltaan pyörähdysparaboloidi.

Tehtävä

Laske peilin pinta-ala peilin ja x-akselin leikkauskohdan funktiona, kun peili rajoitetaan siten, että se ei ulotu lampun etupuolelle. Millainen peilin tulee olla, jotta sen pinta-ala olisi 10 yksikköä?