Differentiaaliyhtälö antaa melkoisesti tietoa ratkaisukäyristä ilman, että sitä on tarpeen ratkaista.
Normaalimuodossa oleva ensimmäisen kertaluvun yhtälö
y' = f(x, y)
ilmaisee suoraan pisteen (x, y) kautta kulkevan ratkaisukäyrän tangenttisuunnan: y' on kulmakerroin. Tämä antaa mahdollisuuden suuntakentän piirtämiseen: xy-tason pistehilassa lasketaan kulmakertoimien arvot ja nämä ilmaistaan graafisessa esityksessä lyhyillä janoilla. Tulos antaa jo varsin hyvän kuvan ratkaisukäyrien muodostamasta parvesta.
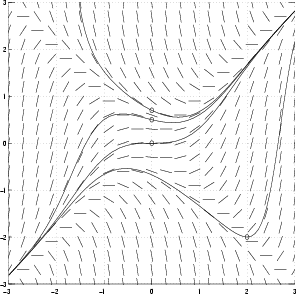
Oheinen kuvio on yhtälöä y' = x2 - y2 vastaava suuntakenttä, jossa on muutamia ratkaisukäyriä.

Ne xy-tason käyrät, joilla ratkaisukäyrien kaltevuudella on vakioarvo, ovat differentiaaliyhtälön isokliinejä. Näiden yhtälö on muotoa f(x, y) = p, missä p on kaltevuutta osoittava vakio. Erityisesti käyrän f(x, y) = 0 pisteissä differentiaaliyhtälön ratkaisukäyrillä on vaakasuora tangentti.
Alueessa, missä f(x, y) > 0, ovat differentiaaliyhtälön ratkaisufunktiot kasvavia; jos f(x, y) < 0, ne ovat väheneviä.
Jos funktio f(x, y) on määritelty koko tarkastelualueessa, saadaan jokaiseen pisteeseen yksikäsitteinen tangenttisuunta. Eri ratkaisukäyrät eivät tällöin voi leikata toisiaan (mutta voivat sivuta).