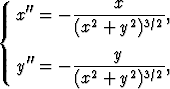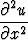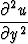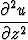Differentiaaliyhtälö
Differentiaaliyhtälöksi kutsutaan yhtälöä, jossa tuntemattomana on funktio ja joka
sisältää tämän funktion derivaattoja. Yhtälön tulee olla voimassa kaikilla muuttujan
arvoilla, jotka kuuluvat johonkin alueeseen, esimerkiksi koko reaaliakselille, jollekin sen
avoimelle välille tms.
Jos tuntematon funktio on yhden muuttujan funktio, esimerkiksi y(x), puhutaan
tavallisesta differentiaaliyhtälöstä.
Esimerkkejä tavallisista differentiaaliyhtälöistä ovat
| y' = cos x, | | x 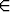 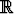 , , | | | |
|
| y'' + 4y = 0, | | x 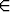 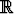 , , | | | |
|
| x2y'' - xy' - y = 0, | | x > 0, | | | |
|
| y' = x3e-y, | | missä on vaikeampi ilmaista aluetta, jossa ratkaisua haetaan. | | | | |
Näissä muuttuja voidaan luonnollisesti kirjoittaa näkyviinkin: y'(x) = cos x,
y''(x) + 4y(x) = 0 jne.
Muuttujan symbolina voi x:n ohella olla mikä tahansa sopiva kirjain. Usein käytössä
on t, jos taustana on sovellustehtävä, jossa riippumaton muuttuja tarkoittaa
aikaa.
Tarkastelun kohteena voi olla myös differentiaaliyhtälöryhmä, jolloin yhtälöitä ja
tuntemattomia funktioita on yhtä monta. Esimerkkinä olkoon taivaanmekaniikkaan
liittyvä yhtälöryhmä
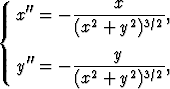
missä tuntemattomat funktiot ovat x(t) ja y(t).
Jos tuntematon funktio on usean muuttujan funktio, esimerkiksi u(x, y, z), kyseessä on
osittaisdifferentiaaliyhtälö. Yhtälössä esiintyvät derivaatat ovat tällöin funktion u
osittaisderivaattoja muuttujien (esimerkkitapauksessa x, y, z) suhteen. Yhtälön tulee olla
voimassa jossakin sopivassa alueessa, esimerkiksi kolmiulotteisen avaruuden pallossa
{(x, y, z) | x2 + y2 + z2 < 1}.
Tyypillinen esimerkki osittaisdifferentiaaliyhtälöstä on Laplacen differentiaaliyhtälö
uxx + uyy + uzz = 0,
missä alaindeksit viittaavat toisen kertaluvun osittaisderivaattoihin. Tätä voidaan myös
merkitä
uxx (x, y, z) + uyy(x, y, z) + uzz(x, y, z) = 0 tai 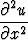 +
+ 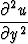 +
+ 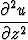 = 0.
= 0.
Osittaisdifferentiaaliyhtälöitä ei tässä enempää käsitellä.
SKK 15.5.2001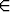
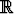 ,
,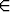
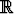 ,
,