| y'(t) = ay(t) - by(t)2 | = | b( y(t) - y(t)2) |
| = | by(t)( - y(t)) > 0, |
y'(t) = ay(t) - by(t)2,
missä a > b > 0. Oletetaan, että y(t)
]0, 
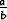[ jokaisella t > 0. Osoita yhtälöä
ratkaisematta, että y on aidosti kasvava. Jos populaation kasvunopeus y'(t) on
suurimmillaan hetkellä t0 > 0, niin mikä on populaation määrä y(t0) hetkellä t0? 
(oletuksessa b > 0), niin
| y'(t) = ay(t) - by(t)2 | = | b(y(t) - y(t)2) |
| = | by(t)( - y(t)) > 0, |
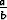> y(t) > 0. Täten y on aidosti kasvava.
Jos y'(t0) on suurin kasvunopeus, niin y''(t0) = 0. Tästä saadaan
| ay'(t0) - 2by(t0)y'(t0) | = | 0 |
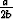
| y'(t0)(a - 2by(t0)) | = | 0 , |
]0, 
[.
| Piilota ratkaisu |