Ikkunan pinta-ala
Arkkitehtiosastojen valintakoetehtävä vuodelta 1991
Ikkuna muodostuu suorakaiteesta ja
sen yläpuolella olevasta puoliympyrästä, jonka halkaisija on sama kuin suorakaiteen
leveys. Mikä on ikkunan suurin mahdollinen pinta-ala, kun sen ympärysmitta on 6.0 m?
Anna vastaus yhden desimaalin tarkkuudella.
Ratkaisu
Olkoot suorakaiteen sivut a ja 2x, missä x on sen puoliympyrän säde, jonka
halkaisija muodostaa suorakaiteen sivun 2x. Jos p on annettu piiri, niin p = 2x + 2a + 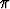 x.
Tällöin pinta-alalle
x.
Tällöin pinta-alalle
A(x) = 2xa + 
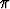 x2 = px -
x2 = px -  (4 +
(4 + 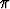 )x2
)x2
A'(x) = p - (4 + 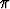 )x.
)x.
Ehdosta A'= 0 saadaan
x =  .
.
Koska A':n merkki vaihtuu +  - (tai koska A'' < 0), x on maksimikohta. Tällöin, kun p
= 4 m,
- (tai koska A'' < 0), x on maksimikohta. Tällöin, kun p
= 4 m,
Amax = 
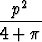 =
= 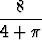
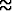 1.1m2.
1.1m2.

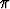 x2 = px -
x2 = px -  (4 +
(4 + 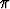 )x2
)x2
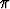 x.
Tällöin pinta-alalle
x.
Tällöin pinta-alalle

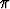 x2 = px -
x2 = px -  (4 +
(4 + 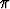 )x2
)x2
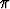 )x.
)x.
 .
.
 - (tai koska A'' < 0), x on maksimikohta. Tällöin, kun p
= 4 m,
- (tai koska A'' < 0), x on maksimikohta. Tällöin, kun p
= 4 m,

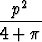 =
= 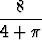
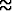 1.1m2.
1.1m2.