Kivikuulapyramidi
Arkkitehtiosastojen valintakoetehtävä vuodelta 1997
Kivikuulapyramidi muodostetaan
neljästä kuulasta siten, että yksi kuula asetetaan kolmen maata koskettavan kuulan
päälle. Lisäksi kaikki kuulat koskettavat toisiaan. Laske pyramidin (tarkka) korkeus, kun
jokaisen kuulan halkaisija on 1 (pituusyksikköä)?
Ratkaisu
Kuulien keskipisteet A, B, C ja D muodostavat säännöllisen tetraedrin. Olkoot
 ACD tetraedrin pohjakolmio ja B tetraedrin huippu.
Tällöin tetraedrin korkeus h on sama kuin kolmiossa
ACD tetraedrin pohjakolmio ja B tetraedrin huippu.
Tällöin tetraedrin korkeus h on sama kuin kolmiossa  ABE sivulle AE piirretyn
korkeusjanan pituus, missä E on tetraedrin särmän CD keskipiste. Koska |AB| = 1 ja
|BE| = |AE| =
ABE sivulle AE piirretyn
korkeusjanan pituus, missä E on tetraedrin särmän CD keskipiste. Koska |AB| = 1 ja
|BE| = |AE| = 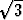 /2, niin korkeudelle h pätee yhtälö
/2, niin korkeudelle h pätee yhtälö
 =
=  +
+ 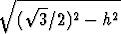 .
.
Tästä h = 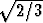 , joten pyramidin korkeus on 1 + h = 1 -
, joten pyramidin korkeus on 1 + h = 1 -  .
.

 ACD tetraedrin pohjakolmio ja B tetraedrin huippu.
ACD tetraedrin pohjakolmio ja B tetraedrin huippu.

 ABE sivulle AE piirretyn
korkeusjanan pituus, missä E on tetraedrin särmän CD keskipiste. Koska |AB| = 1 ja
|BE| = |AE| =
ABE sivulle AE piirretyn
korkeusjanan pituus, missä E on tetraedrin särmän CD keskipiste. Koska |AB| = 1 ja
|BE| = |AE| = 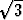 /2, niin korkeudelle h pätee yhtälö
/2, niin korkeudelle h pätee yhtälö
 =
=  +
+ 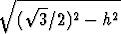 .
.
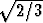 , joten pyramidin korkeus on 1 + h = 1 -
, joten pyramidin korkeus on 1 + h = 1 -  .
.