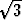 . Jos varasto on
mahdollisimman täynnä, ei sisemmän pallonkuoren sisällä ole ollenkaan tyhjää. Koska
sisemmän pallonkuoren sisään jäävä tilavuus on
. Jos varasto on
mahdollisimman täynnä, ei sisemmän pallonkuoren sisällä ole ollenkaan tyhjää. Koska
sisemmän pallonkuoren sisään jäävä tilavuus on  .
. 
 R
R = 496860.3 . . . , ei suurin
mahdollinen kuutioiden lukumäärä voi olla alle 496 861.
= 496860.3 . . . , ei suurin
mahdollinen kuutioiden lukumäärä voi olla alle 496 861. Olkoon R = 100a. Haluamme tietää, ainakin likimäärin, kuinka monta laatikkoa varastoon mahtuu. Osoita, että suurin mahdollinen laatikoiden lukumäärä ei voi olla yli 523 598 eikä alle 496 861 kappaletta. (Oikein perusteltu pienempi yläraja ja suurempi alaraja tietenkin hyväksytään.)
 -pallo, jonka säde on R = 100 ja tilavuus siis
-pallo, jonka säde on R = 100 ja tilavuus siis
 .
. 
 R3 = 523598.7 . . . . Koska yhden kuution tilavuus on 1, niitä siis ei voi mahtua yli 523
598 kappaletta.
R3 = 523598.7 . . . . Koska yhden kuution tilavuus on 1, niitä siis ei voi mahtua yli 523
598 kappaletta.
Ajatellaan varastoa rajoittavan pallonkuoren sisään toinen pallonkuori, jonka säde on
yhden kuution lävistäjän verran pienempi kuin R, siis R0 = 100 - 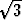 . Jos varasto on
mahdollisimman täynnä, ei sisemmän pallonkuoren sisällä ole ollenkaan tyhjää. Koska
sisemmän pallonkuoren sisään jäävä tilavuus on
. Jos varasto on
mahdollisimman täynnä, ei sisemmän pallonkuoren sisällä ole ollenkaan tyhjää. Koska
sisemmän pallonkuoren sisään jäävä tilavuus on  .
. 
 R
R = 496860.3 . . . , ei suurin
mahdollinen kuutioiden lukumäärä voi olla alle 496 861.
= 496860.3 . . . , ei suurin
mahdollinen kuutioiden lukumäärä voi olla alle 496 861.
| Piilota ratkaisu |