Lasikäytävä
Arkkitehtiosastojen valintakoetehtävä vuodelta 1993
Kauppakeskukseen suunnitellaan
kahta tavarataloa yhdistävää lasisin kattolevyin verhottua käytävää. Katon
poikkileikkauskuvio on puoliympyrä, jonka säde r on 10 m.
Katon levyt taivutetaan tehtaalla pituussuunnassa katon ympyrämuotoon.
Valmistustekniikasta johtuen levyn pitkän sivun pituuden l on oltava vähintään 3.5 m,
enintään 5 m ja jaollinen 50 cm:llä. Lisäksi kaikkien levyjen tulee olla päällekkäin
vähintään 20 cm:n matkalta ja että ylimmäksi asetettava levy ulottuu yhtä paljon harjan
kummallekin puolelle. Kuinka pitkiä levyjä on tilattava, kun yhden levyn hinta on
suoraan verrannollinen levyn pituuteen ja kun halutaan päästä mahdollisimman halvalla.
Ratkaisu
Olkoon l levyn pituus ja d päällekkäinmenevän osan pituus (> 0.2 m). Tällöin,
jos n on kokonaisten levyjen lukumäärä neljännesympyrässä, on
n(l - d) + 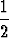 l =
l = 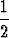
 r (r = 10).
r (r = 10).
Siten
nd = (n +  )l -
)l - 
 r.
r.
Kattaminen on edullisinta, kun nd on pienin (ehdolla nd > 0.2n). Optimipituus levylle
löydetään kokeilemalla:
| jos | l = 3.5 m, | on oltava | n > 5, | jolloin | 5d = 3.54 m |
| jos | l = 4 m, | on oltava | n > 4, | jolloin | 4d = 2.29 m |
| jos | l = 4.5 m, | on oltava | n > 4, | jolloin | 4d = 4.54 m |
| jos | l = 5 m, | on oltava | n > 3, | jolloin | 3d = 1.79 m |
|
Edullisinta on, jos levyn pituus on 5 m.


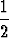 l =
l = 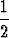
 r (r = 10).
r (r = 10).
 )l -
)l - 
 r.
r.