| A = ”A voitaa pelin” |  = ”A häviää pelin” = ”A häviää pelin” |
|
| B = ”B voitaa pelin” |  = ”B häviää pelin” = ”B häviää pelin” |
|
| C = ”C voitaa pelin” |  = ”C häviää pelin”. = ”C häviää pelin”. |
| A = ”A voitaa pelin” |  = ”A häviää pelin” = ”A häviää pelin” |
|
| B = ”B voitaa pelin” |  = ”B häviää pelin” = ”B häviää pelin” |
|
| C = ”C voitaa pelin” |  = ”C häviää pelin”. = ”C häviää pelin”. |
P (A) = P (B) = P (C) =  .
.
| 1. | A  | |||
| 2. |  B B | |||
| 3. |  B B | |||
| 4. |  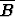 C C | A  |   C C |   C C |
| 5. |   C C |   C C | A  |   C C |
| 6. |  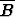 C C | 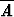  C C |   C C | A 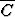 |
| 7. | 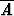  C C |   C C |   C C |
P (henkilö C voittaa kolme peliä) = ( )3 + 3 . (
)3 + 3 . ( )4 =
)4 = 
 0.074.
0.074.
| Piilota ratkaisu |