Myynnin arvo
Syksyn pitkän matematiikan ylioppilastehtävä vuodelta 1994
Jos kauppias alentaa
tuotteen hintaa p %, tuotetta myydään 1.6p % enemmän. Mikä p:n arvo antaa kauppiaalle
suurimman myynnin arvon? Millä p:n arvolla myynnin arvo on sama kuin alkuperäisellä
hinnalla?
Ratkaisu
Olkoon tuotteen alkuperäinen hinta a, ja alkuperäinen myynnin määrä m.
Tällöin alennettu hinta on
a - 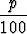 = a(1 -
= a(1 - 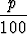 )
)
ja kasvanut myynnin määrä on
m + 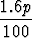 m = m(1 +
m = m(1 + 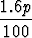 ).
).
Kuvataan myynnin arvon riippuvuutta annetun prosentin p avulla funktiolla
f(p) = a(1 -  ) . m(1 +
) . m(1 +  ).
).
Funktion ääriarvoja voidaan etsiä välin alkupisteestä (p > 0) ja funktion derivaatan
nollakohdista:
f'(p) = am(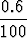 -
-  ) = 0, kun p = 18.75.
) = 0, kun p = 18.75.
Koska p = 18.75 on kuvaajana olevan alaspäin aukeavan paraabelin huipun argumentti,
niin alkuperäistä hintaa (p = 0) ja huipun suhteen symmetristä toista nollakohtaa
2p = 2 . 18.75 = 37.5 vastaavien myynnin arvojen täytyy olla samat ts. f(0) = f(37.5).
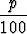 = a(1 -
= a(1 - 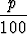 )
)
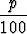 = a(1 -
= a(1 - 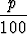 )
)
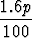 m = m(1 +
m = m(1 + 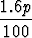 ).
).
 ) . m(1 +
) . m(1 +  ).
).
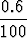 -
-  ) = 0, kun p = 18.75.
) = 0, kun p = 18.75.