
 |
 . Miten kulma
. Miten kulma on valittava, jotta poikkileikkauksen pinta-ala (ja näin
myös rännin tilavuus) tulisi mahdollisimman suureksi?
on valittava, jotta poikkileikkauksen pinta-ala (ja näin
myös rännin tilavuus) tulisi mahdollisimman suureksi?  ja x = scos
ja x = scos  . Tällöin poikkileikkauksen ala
on
. Tällöin poikkileikkauksen ala
on
f( ) = (s + x)h = s2(sin
) = (s + x)h = s2(sin  + cos
+ cos  sin
sin  ),
),
missä 0 <  <
<  /2. Ehdosta f'(
/2. Ehdosta f'( ) = 0 saadaan cos
) = 0 saadaan cos  =
= 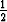 tai -1. Näistä -1 ei kelpaa,
koska 0 <
tai -1. Näistä -1 ei kelpaa,
koska 0 <  <
<  /2 ja cos
/2 ja cos  > 0. Yhtälö cos
> 0. Yhtälö cos  =
= 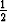 antaa
antaa  =
=  /3 (= 60o). Esimerkiksi
f':n merkkivaihtelun perusteella
/3 (= 60o). Esimerkiksi
f':n merkkivaihtelun perusteella  =
=  /3 on paikallinen maksimikohta. Todetaan että se
myös antaa funktion f suurimman arvon välillä 0 <
/3 on paikallinen maksimikohta. Todetaan että se
myös antaa funktion f suurimman arvon välillä 0 <  <
<  /2. Siten vastaus on
/2. Siten vastaus on  =
=  /3.
/3.
| Piilota ratkaisu |