Pullon piilotusta
Insinööriosastojen valintakoetehtävä vuodelta 1997
Jeppe Niilonpoika on löytänyt
pullolleen hienon piilopaikan hyllyn suorakulmaisesta nurkasta kahden suuren
sylinterinmuotoisen maalipurkin takaa. Kuinka suuri voi täysin näkymättömissä olevan
pullon halkaisija d enintään olla, kun kummankin maalipurkin halkaisja on (tarkasti) 2
dm?
Ilmoita pullon halkaisijan tarkka arvo (desimetreissä) ja likiarvo millimetreissä yhden
yksikön tarkkuudella.
Ratkaisu
Olkoon pullon säde r(= d/2). Pythagoraan lauseen avulla on todettavissa, että
etäisyys pullon keskipisteestä nurkkaan on r , ja etäisyys purkkien sivuamispisteestä -
olkoon se piste C pisteeseen, jossa purkkien keskipisteiden kautta kulkeva suora kohtaa
(jommankumman) seinän, on 1 +
, ja etäisyys purkkien sivuamispisteestä -
olkoon se piste C pisteeseen, jossa purkkien keskipisteiden kautta kulkeva suora kohtaa
(jommankumman) seinän, on 1 +  . Koska viimeksi mainittu etäisyys on sama kuin
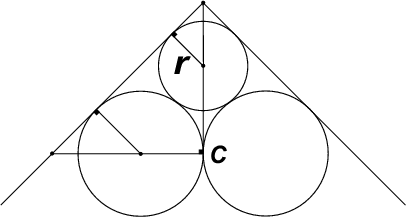
etäisyys pisteestä C hyllynn nurkkaan, nähdään, että etäisyys pisteestä C pullon
keskipisteeseen on 1 +
. Koska viimeksi mainittu etäisyys on sama kuin
etäisyys pisteestä C hyllynn nurkkaan, nähdään, että etäisyys pisteestä C pullon
keskipisteeseen on 1 +  - r
- r .
Soveltamalla Pythagoraan lausetta suorakulmaiseen kolmioon, jonka kärjet ovat pullon ja
toisen purkin keskipisteissä sekä pisteessä C saadaan yhtälö
.
Soveltamalla Pythagoraan lausetta suorakulmaiseen kolmioon, jonka kärjet ovat pullon ja
toisen purkin keskipisteissä sekä pisteessä C saadaan yhtälö
12 + (1 +  - r
- r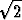 )2 = (1 + r)2,
)2 = (1 + r)2,
josta ratkaisemalla saadaan r = 3 + 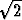 -
- 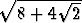 (yhtälön toinen juuri antaisi
sellaisen pullon säteen, joka sijoitettuna purkkien eteen sivuaisi niitä ja seiniä). Kysytty
halkaisja on siis
(yhtälön toinen juuri antaisi
sellaisen pullon säteen, joka sijoitettuna purkkien eteen sivuaisi niitä ja seiniä). Kysytty
halkaisja on siis
d = 2r = 6 + 2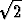 - 4
- 4 (dm)
(dm)  144 mm.
144 mm.


 , ja etäisyys purkkien sivuamispisteestä -
olkoon se piste C pisteeseen, jossa purkkien keskipisteiden kautta kulkeva suora kohtaa
(jommankumman) seinän, on 1 +
, ja etäisyys purkkien sivuamispisteestä -
olkoon se piste C pisteeseen, jossa purkkien keskipisteiden kautta kulkeva suora kohtaa
(jommankumman) seinän, on 1 +  . Koska viimeksi mainittu etäisyys on sama kuin
etäisyys pisteestä C hyllynn nurkkaan, nähdään, että etäisyys pisteestä C pullon
keskipisteeseen on 1 +
. Koska viimeksi mainittu etäisyys on sama kuin
etäisyys pisteestä C hyllynn nurkkaan, nähdään, että etäisyys pisteestä C pullon
keskipisteeseen on 1 +  - r
- r .
.
 - r
- r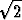 )2 = (1 + r)2,
)2 = (1 + r)2,
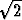 -
- 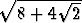 (yhtälön toinen juuri antaisi
sellaisen pullon säteen, joka sijoitettuna purkkien eteen sivuaisi niitä ja seiniä). Kysytty
halkaisja on siis
(yhtälön toinen juuri antaisi
sellaisen pullon säteen, joka sijoitettuna purkkien eteen sivuaisi niitä ja seiniä). Kysytty
halkaisja on siis
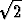 - 4
- 4 (dm)
(dm)  144 mm.
144 mm.