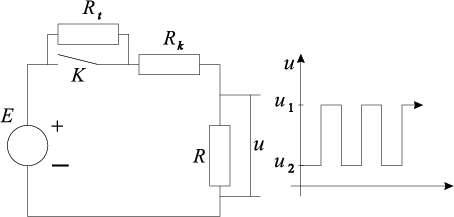
 |
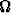 ja
Rt = 1944
ja
Rt = 1944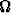 ? Ilmoita myös, mikä on erotuksen u suurin arvo.
? Ilmoita myös, mikä on erotuksen u suurin arvo.
u(R) = u1(R) - u2(R) =  -
-  (R > 0)
(R > 0)
u'(R) = 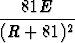 -
- 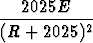 .
.
 = 9 . 45 = 405. Derivaatan u'(R) merkin vaihtumisen perusteella
erotusfunktio u(R) saavuttaa paikallisen maksimin tällä arvolla. Koska u'(R) > 0 joukossa
[0, 450], u(R) on kasvava arvoa R = 450 pienemmillä vastuksen arvoilla. Vastaavasti u'(R)
on vähenevä suuremmilla arvoilla. Siten erotusfunktio u(R) saavuttaa suurimman
arvonsa, kun R = 450
= 9 . 45 = 405. Derivaatan u'(R) merkin vaihtumisen perusteella
erotusfunktio u(R) saavuttaa paikallisen maksimin tällä arvolla. Koska u'(R) > 0 joukossa
[0, 450], u(R) on kasvava arvoa R = 450 pienemmillä vastuksen arvoilla. Vastaavasti u'(R)
on vähenevä suuremmilla arvoilla. Siten erotusfunktio u(R) saavuttaa suurimman
arvonsa, kun R = 450 . Ilmeisesti suurin arvo on u(450) =
. Ilmeisesti suurin arvo on u(450) = 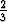 E.
E.
| Piilota ratkaisu |