Suppilo
Arkkitehtiosastojen valintakoetehtävä vuodelta 1997
Suoran ympyräpohjaisen
kartion muotoinen suppilo voidaan tehdä paperista siten, että ympyränmuotoisesta
paperinpalasta leikataan pois  -kulmainen sektori ja reunat teipataan yhteen.
Millä kulman
-kulmainen sektori ja reunat teipataan yhteen.
Millä kulman  arvolla suppilon tilavuus tulee mahdollisimman suureksi? Ilmoita
kulman tarkka arvo radiaaneissa ja likiarvo asteissa yhden yksikön tarkkuudella.
arvolla suppilon tilavuus tulee mahdollisimman suureksi? Ilmoita
kulman tarkka arvo radiaaneissa ja likiarvo asteissa yhden yksikön tarkkuudella.
Ratkaisu
Olkoot r, h ja R muodostettavan kartionmuotoisen suppilon (lyhyesti kartion)
pohjaympyrän säde, korkeus ja reunaviivan pituus. Nyt R on myös sen ympyrän säde,
jonka kokoisesta paperinpalasta kartion vaippaa aletaan muodostaa.
Ilmeisesti r2 + h2 = R2. Tällöin maksimoitava tilavuus on
V (h) = 
 r2h =
r2h = 
 (R2 - h2)h, h
(R2 - h2)h, h  [0, R].
[0, R].
Nyt V '(h) = 
 (R2 - 3h2) = 0, kun h = R/
(R2 - 3h2) = 0, kun h = R/
 [0, R], ja koska V (0) = 0 = V (R) ja
V (R/
[0, R], ja koska V (0) = 0 = V (R) ja
V (R/ ) > 0, niin V (h) saavuttaa maksimin, kun h = R/
) > 0, niin V (h) saavuttaa maksimin, kun h = R/ .
.
Koska kartion pohjaympyrän kehän pituudelle on
2 r = 2
r = 2
 = 2
= 2 R
R = (2
= (2 -
-  )R
)R
poisleikattavan sektorin kulmaksi tulee  = 2
= 2 (1 -
(1 -  ) rad eli 66o.
) rad eli 66o.

 -kulmainen sektori ja reunat teipataan yhteen.
-kulmainen sektori ja reunat teipataan yhteen.

 arvolla suppilon tilavuus tulee mahdollisimman suureksi? Ilmoita
kulman tarkka arvo radiaaneissa ja likiarvo asteissa yhden yksikön tarkkuudella.
arvolla suppilon tilavuus tulee mahdollisimman suureksi? Ilmoita
kulman tarkka arvo radiaaneissa ja likiarvo asteissa yhden yksikön tarkkuudella. 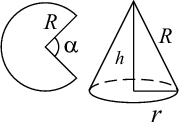

 r2h =
r2h = 
 (R2 - h2)h, h
(R2 - h2)h, h  [0, R].
[0, R].

 (R2 - 3h2) = 0, kun h = R/
(R2 - 3h2) = 0, kun h = R/
 [0, R], ja koska V (0) = 0 = V (R) ja
V (R/
[0, R], ja koska V (0) = 0 = V (R) ja
V (R/ ) > 0, niin V (h) saavuttaa maksimin, kun h = R/
) > 0, niin V (h) saavuttaa maksimin, kun h = R/ .
.
 r = 2
r = 2
 = 2
= 2 R
R = (2
= (2 -
-  )R
)R
 = 2
= 2 (1 -
(1 -  ) rad eli 66o.
) rad eli 66o.