 ) =
) =  +
+  , missä 0 <
, missä 0 <  <
< 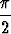 .
.
l( ) =
) =  +
+  , missä 0 <
, missä 0 <  <
< 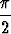 .
.
l'( ) = -
) = - +
+ 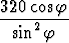 .
.
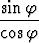 =
= 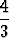 eli tan
eli tan  =
= 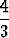 .
.
 0 = arctan
0 = arctan  kuuluu välille 0 <
kuuluu välille 0 <  <
<  . Funktio on vähenevä välillä
]
. Funktio on vähenevä välillä
] ,
,  0[ ja kasvava välillä ]
0[ ja kasvava välillä ] 0,
0,  [, joten funktio saa minimiarvonsa, kun
[, joten funktio saa minimiarvonsa, kun  =
=  0.
Funktion l minimiarvo on tällöin 625. Kysytty tangon pituus saadaan projektion
korkeudesta (h = 250) Pythagoraan lauseen avulla: tangon pituus =
0.
Funktion l minimiarvo on tällöin 625. Kysytty tangon pituus saadaan projektion
korkeudesta (h = 250) Pythagoraan lauseen avulla: tangon pituus = 
 673
(cm).
673
(cm).
Laskentaohjelmaa käytettäessä derivaatan ja sen nollakohtien lausekkeet saattavat olla hyvinkin erilaisessa muodossa kuin yllä olevat, mutta oikea vastaus on luonnollisesti sama.
| Piilota ratkaisu |