

|
Tikkaa heitetään tauluun tähtäämättä tarkemmin kohti keskustaa. Laske todennäköisyys
sille, että tauluun osuneella tikalla saadaan tulokseksi
a) kymmenen
b) seitsemän tai kahdeksan.
 R2. Todennäköisyys saada tulokseksi
kymmenen P ({10}) on tätä tulosta vastaavan taulun pinta-alan suhde koko taulun
alaan.
R2. Todennäköisyys saada tulokseksi
kymmenen P ({10}) on tätä tulosta vastaavan taulun pinta-alan suhde koko taulun
alaan.
P ({10}) = 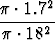 =
=  = 0.0089
= 0.0089 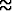 0.9 %.
0.9 %.
 . 6.82 -
. 6.82 -  . 3.42. Jakamalla saatu pinta-ala koko taulun
pinta-alalla saadaan todennäköisyydeksi P ({7, 8}) = 0.107 = 10.7 %.
. 3.42. Jakamalla saatu pinta-ala koko taulun
pinta-alalla saadaan todennäköisyydeksi P ({7, 8}) = 0.107 = 10.7 %.
Todennäköisyyttä, että osumakohta on korkeintaan x cm päässä taulun keskipisteestä kuvaa kertymäfunktio
F (x) = F (X < x) =  =
= 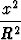 .
.
P ({10}) = P (0 < x < 1.7) = F (1.7) - F (0) = 
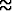 0.9 %.
0.9 %.
P ({7, 8}) = P (6.8 < x < 3.4) = F (6.8) - F (3.4) = 
 10.7 %.
10.7 %.
| Piilota ratkaisu |