,
Suuren maatalon tupa on suorakulmion muotoinen (6 m x 5 m). Tuvan kattoon voidaan kiinnittää ainoastaan yksi lamppu ja se halutaan sen vuoksi asettaa keskelle kattoa. Mille korkeudelle lamppu on kiinnitettävä, jotta tuvan perimmäisessäkin nurkassa olisi mahdollisimman paljon valoa? Huoneen korkeus on 250 cm.
Pistemmäinen valolähde, jonka valovoimakkuus on I, antaa etäisyydellä r olevalle pinnalle valaistuksen
E = ,
on valonsäteen ja lattian normaalin välinen kulma. 
. Lampun etäisyys r tuvan nurkasta
voidaan lausua lampun sijoituskorkeuden h ja lattian lävistäjän a avulla:
r = 
.
= h/r.
Valaistuksen lauseke saadaan siten muotoon
E(h) = 
.
E'(h) = 
.
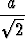. Näistä kumpikaan ei ole välillä [0, 250]. Funktio
E on kasvava välillä [0, 250], joten valaistuksen arvo on suurin kohdassa x = 250
(cm).
Koska huoneen korkeus on 2.5 metriä, lamppua ei käytännössä voi asentaa tarkalleen niin korkealle, vaan se asennetaan niin ylös kuin mahdollista.
| Piilota ratkaisu |