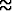 31 poikaa ja tyttöjen lukumäärän
odotusarvo nq = 60 . 0.487
31 poikaa ja tyttöjen lukumäärän
odotusarvo nq = 60 . 0.487 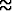 29 tyttöä.
29 tyttöä.
Mitä jakaumaa tyttöjen ja poikien lukumäärät noudattavat? Mikä on poikien ja mikä tyttöjen lukumäärän odotusarvo? Millä todennäköisyydellä syntyy täsmälleen yhtä monta tyttöä ja poikaa?
Merkitään
| Syntyvien lasten lukumäärä | = | n |
| P (lapsi on poika) | = | p |
| P (lapsi on tyttö) | = | 1 - p = q. |
Tällöin saadaan tehtävän asettelusta
| n | = | 60 |
| p | = | 0.513 |
| q | = | 0.487. |
Todennäköisyys, että poikia syntyy täsmälleen määrä k (0 < k < 60), on
P (x = k) = ( n k) . pk . qn-k,
jossa satunnaismuuttuja x kuvaa poikalasten lukumäärää.Poikien lukumäärän odotusarvo on np = 60 . 0.513 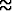 31 poikaa ja tyttöjen lukumäärän
odotusarvo nq = 60 . 0.487
31 poikaa ja tyttöjen lukumäärän
odotusarvo nq = 60 . 0.487 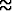 29 tyttöä.
29 tyttöä.
Tyttöjä ja poikia syntyy yhtä monta, kun k = 30 eli
P (x = 30) = (
60
30)
. 0.52330 . 0.48730 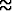 0.100518
0.100518 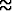 0.10.
0.10.
| Piilota ratkaisu |