Valmistajan voitto

Syksyn pitkän matematiikan ylioppilastehtävä vuodelta 1995

Valmistaja saa myydyksi tuotettaan määrän

m = 400 V~ ------- 50 + p,

kun yhden yksikön hinta on p mk. Tuotemäärän kaikki kustannukset ovat 800 + 2m (mk). Millä p:n arvoilla valmistaja saa voittoa?

Ratkaisu

Myynnin arvo on m . p. Ehto voitolle on, että myynnin arvo on suurempi kuin kustannukset eli

m . p > 800 + 2m.

Tästä voidaan kirjoittaa edelleen epäyhtälö ja sieventää sitä:

V~ 400-- 50+p . p>800 + 2 .  V~ 400- 50+p
400p>800 V~ ------- 50 + p + 800
400p - 800>800 V~ ------- 50 + p
160000p2 - 1280000p - 31360000>0
p2 - 8p - 196>0.

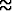Vastaavan 2.asteen yhtälön ratkaisut ovat p1 ~~ -10.56 ja p2 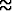~~ 18.56. Merkkiparaabeli aukeaa ylöspäin, joten epäyhtälön ehto toteutuu, kun p < p1 tai p > p2. Näistä jälkimmäinen tuo mielekkään vastauksen.

Käytännössä alueelle, jolla tehtävässä annettu malli myynnin riippuvuudelle hinnasta pätee, on oltava jokin äärellinen yläraja. Muuten yksikköhinnan kasvattaminen äärettömän suureksi mahdollistaisi myös äärettömän suuren voiton.

Piilota ratkaisu