Vesikouru
Arkkitehtiosastojen valintakoetehtävä vuodelta 1995
Pitkästä peltilevystä (leveys 4a)
taivutetaan ylhäältä avoin vesikouru, jonka pystyseinien korkeus on a ja jonka pohja on
v-kirjaimen muotoinen.
Määritä kourun pohjan avautumiskulma  siten, että kourun poikkileikkauksen
pinta-ala on mahdollisimman suuri. Anna vastaus yhden asteen tarkkuudella.
siten, että kourun poikkileikkauksen
pinta-ala on mahdollisimman suuri. Anna vastaus yhden asteen tarkkuudella.
Ratkaisu
Olkoon 2x (0 < x < a) kourun pystyseinien välinen etäisyys. Tällöin kourun
poikkileikkaus voidaan jakaa suorakulmioon, jonka leveys on 2x ja korkeus a, ja
tasakylkiseen kolmioon, jonka kanta on 2x ja korkeus 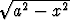 . Poikkileikkauksen
pinta-ala on
. Poikkileikkauksen
pinta-ala on
A(x) = 2ax + x .
.
Tämä saavuttaa suurimman arvonsa derivaatan nollakohdissa tai x:n vaihteluvälin
päätepisteissä. Koska
A'(x) = 2a +  - x2/
- x2/ ,
,
ainoa mahdollinen derivaatan nollakohta on x0 =  a. Laskemalla todetaan, että
A(x) on suurempi kuin A(0) ja A(a), joten x0 tuottaa suurimman poikkileikkauksen
pinta-alan. Koska sin (
a. Laskemalla todetaan, että
A(x) on suurempi kuin A(0) ja A(a), joten x0 tuottaa suurimman poikkileikkauksen
pinta-alan. Koska sin ( /2) = x/a, arvoa x = x0, vastaava avautumiskulma on
/2) = x/a, arvoa x = x0, vastaava avautumiskulma on 
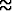 137o.
137o.


 siten, että kourun poikkileikkauksen
pinta-ala on mahdollisimman suuri. Anna vastaus yhden asteen tarkkuudella.
siten, että kourun poikkileikkauksen
pinta-ala on mahdollisimman suuri. Anna vastaus yhden asteen tarkkuudella. 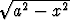 . Poikkileikkauksen
pinta-ala on
. Poikkileikkauksen
pinta-ala on
 .
.
 - x2/
- x2/ ,
,
 a. Laskemalla todetaan, että
A(x) on suurempi kuin A(0) ja A(a), joten x0 tuottaa suurimman poikkileikkauksen
pinta-alan. Koska sin (
a. Laskemalla todetaan, että
A(x) on suurempi kuin A(0) ja A(a), joten x0 tuottaa suurimman poikkileikkauksen
pinta-alan. Koska sin ( /2) = x/a, arvoa x = x0, vastaava avautumiskulma on
/2) = x/a, arvoa x = x0, vastaava avautumiskulma on 
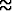 137o.
137o.