Vesisäiliö ja pumppu
Insinööriosastojen valintakoetehtävä vuodelta 1991
Pitkässä suorakulmaisessa säiliössä,
jonka leveys on 3.0 m, on pituussuunnassa liikkuva pystysuora väliseinä. Se jakaa säiliön
osiin A ja B. Vettä pumpataan osaan A nopeudella 4.0 m3/min (osa B pysyy tyhjänä).
Samaan aikaan väliseinä liikkuu nopeudella 0.5 m/min siten, että osan B tilavuus
pienenee. Tarkasteluhetkellä, jolloin osassa A on vettä 5.0 m3, vedenpinnan korkeus on 2.0
m. Millä nopeudella vedenpinnan korkeus muuttuu tarkasteluhetkellä? Anna vastaus
yhden desimaalin tarkkuudella (yksikkö m/min.) Ilmoita myös, nouseeko vai laskeeko
vedenpinta.
Ratkaisu
Merkitään:
V (t) = vesimäärä hetkellä t,
h(t) = veden korkeus hetkellä t ja
p(t) = osan A pituus hetkellä t.
Silloin V (t) = 3p(t)h(t).
Voidaan olettaa, että t = 0 on tarkasteluhetki. Silloin, koska V (0) = 5 ja h(0) = 2,
on
p(0) =  =
= 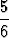 .
.
Siis
| V (t) | = | 5 + 4t | | |
| p(t) | = | 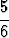 + +  , , | | |
joten
h(t) = 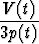 =
=  .
.
Derivoimalla
h'(t) =  .
.
h:n kasvunopeus hetkellä t = 0 on h'(0) =  = 0.4. Pinta siis nousee nopeudella 0.4
m/min.
= 0.4. Pinta siis nousee nopeudella 0.4
m/min.
 =
= 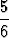 .
.
 =
= 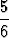 .
.
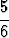 +
+  ,
,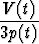 =
=  .
.
 .
.
 = 0.4. Pinta siis nousee nopeudella 0.4
m/min.
= 0.4. Pinta siis nousee nopeudella 0.4
m/min.