Tehtävä 1
Yksinkertaisinta laskea kaikki summat kerralla taulukkoon:
In[1]:=
![]()
Out[1]=
![]()
Funktio FactorInteger jakaa luvun tekijöihin. Sillä on attribuutti Listable, jolloin se voidaan kohdistaa suoraan listaan:
In[2]:=
![]()
Out[2]=
![]()
Tuloksena saadaan kunkin luvun osalta lista alkutekijöistä ja jokaisen kohdalla luku, joka osoittaa tekijän potenssin :
In[3]:=
![]()
Out[3]=
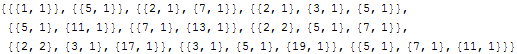
Tuloksena saadaan kolminkertainen lista, joka on hieman vaikealukuinen. Se voidaan kuitenkin tulostaa selkeämpään muotoon:
In[4]:=
![]()
Out[4]//TableForm=
| 1 | {{1,1}} |
| 5 | {{5,1}} |
| 14 | {{2,1},{7,1}} |
| 30 | {{2,1},{3,1},{5,1}} |
| 55 | {{5,1},{11,1}} |
| 91 | {{7,1},{13,1}} |
| 140 | {{2,2},{5,1},{7,1}} |
| 204 | {{2,2},{3,1},{17,1}} |
| 285 | {{3,1},{5,1},{19,1}} |
| 385 | {{5,1},{7,1},{11,1}} |
Funktiolla PrimeQ voidaan selvittää, onko kyseessä alkuluku. PrimeQ on myös Listable.
In[5]:=
![]()
Out[5]=
![]()
Tehtävä 2
Muodostetaan lista lukuja välillä 0-90 astetta:
In[6]:=
![]()
Out[6]=

Lasketaan vastaavat sinin ja kosinin arvot numeerisesti:
In[7]:=
![]()
Out[7]=

In[8]:=
![]()
Out[8]=

Taulukko:
In[9]:=
![]()
Out[9]//TableForm=
| 0 | 0. | 1. |
| 1 | 0.0174524 | 0.999848 |
| 2 | 0.0348995 | 0.999391 |
| 3 | 0.052336 | 0.99863 |
| 4 | 0.0697565 | 0.997564 |
| 5 | 0.0871557 | 0.996195 |
| 6 | 0.104528 | 0.994522 |
| 7 | 0.121869 | 0.992546 |
| 8 | 0.139173 | 0.990268 |
| 9 | 0.156434 | 0.987688 |
| 10 | 0.173648 | 0.984808 |
| 11 | 0.190809 | 0.981627 |
| 12 | 0.207912 | 0.978148 |
| 13 | 0.224951 | 0.97437 |
| 14 | 0.241922 | 0.970296 |
| 15 | 0.258819 | 0.965926 |
| 16 | 0.275637 | 0.961262 |
| 17 | 0.292372 | 0.956305 |
| 18 | 0.309017 | 0.951057 |
| 19 | 0.325568 | 0.945519 |
| 20 | 0.34202 | 0.939693 |
| 21 | 0.358368 | 0.93358 |
| 22 | 0.374607 | 0.927184 |
| 23 | 0.390731 | 0.920505 |
| 24 | 0.406737 | 0.913545 |
| 25 | 0.422618 | 0.906308 |
| 26 | 0.438371 | 0.898794 |
| 27 | 0.45399 | 0.891007 |
| 28 | 0.469472 | 0.882948 |
| 29 | 0.48481 | 0.87462 |
| 30 | 0.5 | 0.866025 |
| 31 | 0.515038 | 0.857167 |
| 32 | 0.529919 | 0.848048 |
| 33 | 0.544639 | 0.838671 |
| 34 | 0.559193 | 0.829038 |
| 35 | 0.573576 | 0.819152 |
| 36 | 0.587785 | 0.809017 |
| 37 | 0.601815 | 0.798636 |
| 38 | 0.615661 | 0.788011 |
| 39 | 0.62932 | 0.777146 |
| 40 | 0.642788 | 0.766044 |
| 41 | 0.656059 | 0.75471 |
| 42 | 0.669131 | 0.743145 |
| 43 | 0.681998 | 0.731354 |
| 44 | 0.694658 | 0.71934 |
| 45 | 0.707107 | 0.707107 |
| 46 | 0.71934 | 0.694658 |
| 47 | 0.731354 | 0.681998 |
| 48 | 0.743145 | 0.669131 |
| 49 | 0.75471 | 0.656059 |
| 50 | 0.766044 | 0.642788 |
| 51 | 0.777146 | 0.62932 |
| 52 | 0.788011 | 0.615661 |
| 53 | 0.798636 | 0.601815 |
| 54 | 0.809017 | 0.587785 |
| 55 | 0.819152 | 0.573576 |
| 56 | 0.829038 | 0.559193 |
| 57 | 0.838671 | 0.544639 |
| 58 | 0.848048 | 0.529919 |
| 59 | 0.857167 | 0.515038 |
| 60 | 0.866025 | 0.5 |
| 61 | 0.87462 | 0.48481 |
| 62 | 0.882948 | 0.469472 |
| 63 | 0.891007 | 0.45399 |
| 64 | 0.898794 | 0.438371 |
| 65 | 0.906308 | 0.422618 |
| 66 | 0.913545 | 0.406737 |
| 67 | 0.920505 | 0.390731 |
| 68 | 0.927184 | 0.374607 |
| 69 | 0.93358 | 0.358368 |
| 70 | 0.939693 | 0.34202 |
| 71 | 0.945519 | 0.325568 |
| 72 | 0.951057 | 0.309017 |
| 73 | 0.956305 | 0.292372 |
| 74 | 0.961262 | 0.275637 |
| 75 | 0.965926 | 0.258819 |
| 76 | 0.970296 | 0.241922 |
| 77 | 0.97437 | 0.224951 |
| 78 | 0.978148 | 0.207912 |
| 79 | 0.981627 | 0.190809 |
| 80 | 0.984808 | 0.173648 |
| 81 | 0.987688 | 0.156434 |
| 82 | 0.990268 | 0.139173 |
| 83 | 0.992546 | 0.121869 |
| 84 | 0.994522 | 0.104528 |
| 85 | 0.996195 | 0.0871557 |
| 86 | 0.997564 | 0.0697565 |
| 87 | 0.99863 | 0.052336 |
| 88 | 0.999391 | 0.0348995 |
| 89 | 0.999848 | 0.0174524 |
| 90 | 1. | 0. |
Tehtävä 3
Kyseessä on kaksinkertainen lista:
In[10]:=
![]()
Out[10]=

Sen matriisimuotoinen esitys (jolloin muuttujaa matriisi ei muuteta, vaan se ainoastaan tulostetaan eri muodossa):
In[11]:=
![]()
Out[11]//MatrixForm=
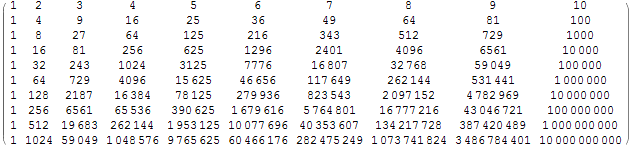
Tehtävä 4
Haetaan 20 ensimmäistä alkulukua:
In[12]:=
![]()
Out[12]=
![]()
Otetaan edellisen taulukon alkiot järjestysluvuiksi ja haetaan näitä vastaavat alkuluvut:
In[13]:=
![]()
Out[13]=
![]()
Koska funktio Prime on Listable, päästään helpommallakin:
In[14]:=
![]()
Out[14]=
![]()
Tehtävä 5
Syötetään annetut vektorit:
In[15]:=
![]()
Funktiolla Solve voidaan ratkaista myös vektoriyhtälöitä:
In[16]:=
![]()
Out[16]=
![]()
Komponentit ovat
In[17]:=
![]()
Out[17]=
![]()
ja näiden summa on todellakin c:
In[18]:=
![]()
Out[18]=
![]()
Tehtävä 6
Syötetään annetut pisteet:
In[19]:=
![]()
Muodostetaan kulman kylkiä esittävät vektorit:
In[20]:=
![]()
Out[20]=
![]()
In[21]:=
![]()
Out[21]=
![]()
Lasketaan kulman puolittajan suuntavektori eo. vektoreiden suuntaisten yksikkövektoreiden summana:
In[22]:=
![]()
Out[22]=
![]()
Vastaava yksikkövektori (vektorin pituuden laskemiseen on myös käytettävissä funktio Norm):
In[23]:=
![]()
Out[23]=
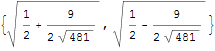
Ehkä tämä on informatiivisempi numeerisena:
In[24]:=
![]()
Out[24]=
![]()
In[25]:=
![]()
Out[25]=
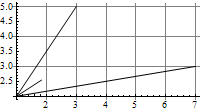
Tehtävä 7
Syötetään annetut avaruuden tason pisteet:
In[26]:=
![]()
Lasketaan niiden väliset vektorit. Nimet viittaavat annettuihin pisteisiin.
In[27]:=
![]()
Tasoa vastaan kohtisuora vektori saadaan ristitulolla:
In[28]:=
![]()
Out[28]=
![]()
Vastaava yksikkövektori:
In[29]:=
![]()
Out[29]=
![]()
Kuvakin voidaan tehdä. Miten tästä näkee, onko tulos oikea?
In[30]:=
![]()
Out[30]=
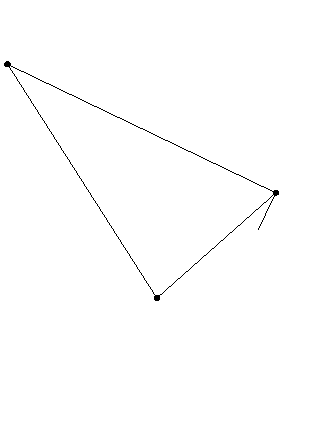
Tehtävä 8
In[31]:=
![]()
Syötetään annettu suora:
In[32]:=
![]()
In[33]:=
![]()
Out[33]=
![]()
Annettu taso:
In[34]:=
![]()
Out[34]=
![]()
Leikkauspiste:
In[35]:=
![]()
Out[35]=
![]()
In[36]:=
![]()
Out[36]=
![]()
Tehtävä 9
Muodostetaan kolmion kärkipisteet:
In[37]:=

Out[37]=
![]()
Out[38]=
![]()
Out[39]=
![]()
Korkeusjanojen AC ja BC leikkauspisteen paikkavektori:
In[40]:=
![]()
Out[40]=
![]()
Sivuille AC ja BC piirrettyjen korkeusjanojen kohtisuoruusehdot:
In[41]:=
![]()
Out[41]=
![]()
In[42]:=
![]()
Out[42]=
![]()
Onko kolmas kohtisuoruusehto voimassa? Funktio Simplify voi saada kaksi argumenttia: ensimmäisenä sievennettävä lauseke, toisena oletuksena oleva ehto:
In[43]:=
![]()
Out[43]=
![]()
Lause on siis todistettu algebrallisesti!
Tehtävä 10
Lähtökohdat:
In[44]:=
![]()
In[45]:=
![]()
In[46]:=
![]()
Kerroinvektori:
In[47]:=
![]()
Out[47]=
![]()
Funktion arvot:
In[48]:=
![]()
Out[48]=
![]()
Integraalin likiarvo:
In[49]:=
![]()
Out[49]=
![]()
Ja sitten kaikki pyydetyt arvot kerralla:
In[50]:=
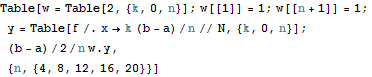
Out[50]=
![]()
Tässä (uloimman) Table-funktion ensimmäinen argumentti — puolipisteellä erotetut komennot — on CompoundExpression. Tällaisen voi aina kirjoittaa yhden komennon sijasta.
Valmiilla numeerisen integroinnin funktiolla tulos on
In[51]:=
![]()
Out[51]=
![]()