a)
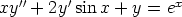
b)
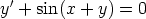
c)
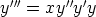
d)
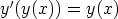
1. Mitkä ovat seuraavien funktiota y = y(x) koskevien differentiaaliyhtälöiden kertaluvut?
Ovatko yhtälöt normaalimuotoisia?
a) 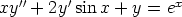
b) 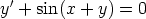
c) 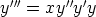
d) 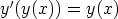
2. Saata differentiaaliyhtälöryhmä
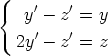
normaalimuotoon.
3. Osoita, että y = 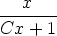 on differentiaaliyhtälön x2y' = y2 yleinen ratkaisu. Määritä
yksittäisratkaisu, joka toteuttaa alkuehdon a) y(1) = 1, b) y(2) = 1. Mitä voidaan sanoa
alkuehdoista c) y(0) = 0 ja d) y(0) = 1? Piirrä ratkaisukäyräparvi.
on differentiaaliyhtälön x2y' = y2 yleinen ratkaisu. Määritä
yksittäisratkaisu, joka toteuttaa alkuehdon a) y(1) = 1, b) y(2) = 1. Mitä voidaan sanoa
alkuehdoista c) y(0) = 0 ja d) y(0) = 1? Piirrä ratkaisukäyräparvi.
4. Osoita, että y = e-2x(C 1 sin x + C2 cos x) on differentiaaliyhtälön y'' + 4y' + 5y = 0 ratkaisu. Määritä ratkaisu, joka toteuttaa alkuehdon a) y(0) = y'(0) = 1, b) y(0) = y'(0) = 0.
5. Osoita, että y = 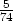 sin x +
sin x + 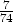 cos x + C1ex + C
2e6x on differentiaaliyhtälön
y'' - 7y' + 6y = sin x yleinen ratkaisu. Laske tehtävä sekä käsin että laskentaohjelmaa
käyttäen.
cos x + C1ex + C
2e6x on differentiaaliyhtälön
y'' - 7y' + 6y = sin x yleinen ratkaisu. Laske tehtävä sekä käsin että laskentaohjelmaa
käyttäen.
6. Osoita, että y = (1 + ln|x|)x on differentiaaliyhtälön x2y''- xy' + y = 0 yksittäisratkaisu, joka toteuttaa alkuehdon y(1) = 1, y'(1) = 2. Laske tehtävä sekä käsin että laskentaohjelmaa käyttäen. Missä alueessa yksittäisratkaisu on määritelty?
7. Osoita, että differentiaaliyhtälöryhmän
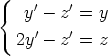
yleinen ratkaisu on y = C1 cos x + C2 sin x, z = (C1 + C2) cos x + (C2 -C1) sin x. Laske tehtävä sekä käsin että laskentaohjelmaa käyttäen.
8. Differentiaaliyhtälöllä y' = y on ratkaisuna y = ex. Osoita, että sen jokainen muu ratkaisu poikkeaa tästä vain kerrannaisella vakiolla. Sijoita tätä varten yrite y = u(x)ex differentiaaliyhtälöön ja johda ehto funktiolle u.
9. Tarkastellaan differentiaaliyhtälöä y''(x) = f(y'(x)). a) Osoita laskentaohjelmaa käyttäen, että käyrä, jonka parametriesitys on
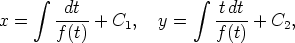
on tämän integraalikäyrä. b) Millä ehdolla differentiaaliyhtälön eräänä ratkaisuna on suora y = ax + b?
10. Muodosta suuntakenttä differentiaaliyhtälölle (x2 - y2)y' = 2xy ja päättele tämän perusteella, millaisia ratkaisukäyrät ovat.
11. Kirjoita differentiaaliyhtälö
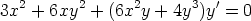
muotoon y' = f(x,y), piirrä suuntakenttä ja tutki yhtälön ratkaisukäyriä tämän avulla.
12. Muodosta suuntakenttä differentiaaliyhtälölle y' = x + y. Määritä niiden käyrien (isokliinien) yhtälöt, joilla suuntaelementtien kaltevuus on vakio p.
13. Määritä differentiaaliyhtälön x2y' = y + 1 isokliinit. Piirrä suuntakenttä.
14. Olkoon funktio f : 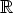 2
2 
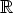 ja sen osittaisderivaatat f
x ja fy jatkuvia. Osoita, että jos
yhtälön y' = f(x,y) ratkaisukäyrällä on käännepiste, niin se sijaitsee käyrällä
ja sen osittaisderivaatat f
x ja fy jatkuvia. Osoita, että jos
yhtälön y' = f(x,y) ratkaisukäyrällä on käännepiste, niin se sijaitsee käyrällä
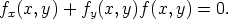
Osoita edelleen, että tämän käyrän pisteissä ratkaisukäyrä ja isokliini sivuavat toisiaan. Tarkastele esimerkkinä yhtälöä y' = x2 - y2 ja määritä tälle em. käyrä sekä isokliinit. Piirrä kuvio.
15. Johda sen käyräparven differentiaaliyhtälö, johon kuuluvat kaikki xy-tason R-säteiset ympyrät. (Parvella on siis kaksi parametria: ympyrän keskipisteen koordinaatit. R on vakio.) Mitä saatu yhtälö ilmaisee parven käyrien kaarevuussäteistä?
16. Etsi käyräparven y = C1x + C2x2 + C 3x3 differentiaaliyhtälö, kun parametreina ovat C 1, C2 ja C3 .
17. Johda sen käyräparven differentiaaliyhtälö, johon kuuluvat kaikki x-akselia origossa sivuavat ympyrät.
18. Tason toisen asteen käyrän yhtälön yleinen muoto on ax2 + by2 + 2cxy + 2dx + 2ey + f = 0. Muodosta kaikkien tällaisten käyrien differentiaaliyhtälö.
19. Palauta differentiaaliyhtälö yy'' + 2y'2 = 0 ensimmäisen kertaluvun normaaliryhmäksi. Onko ryhmä autonominen? Etsi yhtälön yleinen ratkaisu. Piirrä ratkaisukäyrien kuvaajia sekä muuttujan x funktiona että faasitasossa. Määritä faasitasokäyrien yhtälöt.
20. Muodosta differentiaaliyhtälöä (1 -y)y'' + 2y'2 = 0 vastaava normaaliryhmä ja tutki, onko se autonominen. Etsi reunaehtojen y(0) = 0, y(-1) = -1 määräämä ratkaisu ja piirrä sen kuvaaja sekä muuttujan x funktiona että faasitasossa.
21. Totea yhtälö 2y'' = 3y2 autonomiseksi ja piirrä ratkaisukäyrien kuvaajia faasitasoon. Etsi kokeilemalla ratkaisukäyrä, jolla on asymptoottina x-akseli. Miten tämä ilmenee faasitasokuvassa? Etsi kyseisen ratkaisun lauseke.
22. Olkoot x ja y muuttujan t funktioita, joille pätee
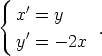
Millaisia ovat ratkaisukäyrät faasitasossa? Johda näiden yhtälöt.
23. Tutki piirtämällä differentiaaliyhtälöryhmän
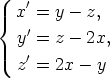
ratkaisuja faasitasossa. Mitä näistä voidaan päätellä pelkän kuvion perusteella? Entä jos kuvioon yhdistetään tieto vakiokertoimisen yhtälön ratkaisun muodosta?
24. Johda yhtälöryhmän
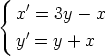
ratkaisujen faasitasoesityksen yhtälöt.
25. Olkoon f : 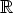 2
2 
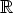 jatkuva kahden muuttujan funktio. Näytä, että differentiaaliyhtälön
y' = yf(x, y) ratkaisukäyrät joko sivuavat x-akselia tai eivät kosketa sitä lainkaan.
jatkuva kahden muuttujan funktio. Näytä, että differentiaaliyhtälön
y' = yf(x, y) ratkaisukäyrät joko sivuavat x-akselia tai eivät kosketa sitä lainkaan.
26. Tutki, missä sijaitsevat differentiaaliyhtälön y' = x + |y| ratkaisukäyrien minimipisteet. Piirrä kuvio ratkaisukäyristä.
27. Palauta toisen kertaluvun differentiaaliyhtälö yy'' + xy' = 0 ensimmäisen kertaluvun normaaliryhmäksi Y ' = F(x,Y ). Millainen vektoriarvoinen funktio F on?
28. Kappaleen (planeetan) liikettä keskeisvoimakentässä hallitsee Newtonin lakien mukainen differentiaaliyhtälö
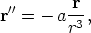
missä pilkut tarkoittavat derivaattoja ajan suhteen, r on paikkavektori, r = |r| tämän pituus ja a vakio. Oletetaan tunnetuksi, että kyseessä on tasoliike, jolloin siis r(t) = x(t) i + y(t) j. Hajota differentiaaliyhtälö komponenttifunktioita x(t) ja y(t) koskevaksi kahden yhtälön ryhmäksi ja palauta tämä neljän yhtälön ensimmäisen kertaluvun ryhmäksi ottamalla nopeuskomponentit uusiksi tuntemattomiksi funktioiksi.
29. Kaksi yksikön suuruista massaa on kiinteästi sidottu pisteisiin (-1, 0) ja (1, 0). Näiden aiheuttamassa gravitaatiokentässä liikkuu kolmas massa. Kirjoita Newtonin lakien mukainen liikeyhtälö ja muodosta vastaava normaaliryhmä. Oletetaan, että kyseessä on tasoliike. Gravitaatiovakiolle käytetään arvoa 1. Tutki numeerisesti, millaisia ratakäyriä malli antaa.
30. Olkoot x(t) ja y(t) tuntemattomat funktiot, m 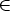
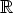 . Muodosta differentiaaliyhtälöryhmää
. Muodosta differentiaaliyhtälöryhmää
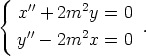
vastaava normaaliryhmä. Tutki piirtämällä ratkaisukäyriä xy-tasossa. Miten nämä
käyttäytyvät, kun t 
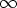 ? Onko yhtälöryhmällä rajoitetuja ratkaisuja? Totea, että
yhtälön ratkaisu on x = emt(C
1 sin mt + C2 cos mt) + e-mt(C
3 sin mt + C4 cos mt),
y = emt (-C
1 cos mt + C2 sin mt) + e-mt(C
3 cos mt - C4 sin mt), jos m
? Onko yhtälöryhmällä rajoitetuja ratkaisuja? Totea, että
yhtälön ratkaisu on x = emt(C
1 sin mt + C2 cos mt) + e-mt(C
3 sin mt + C4 cos mt),
y = emt (-C
1 cos mt + C2 sin mt) + e-mt(C
3 cos mt - C4 sin mt), jos m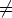 0, ja x = C1 + C2t,
y = C3 + C4 t, jos m = 0.
0, ja x = C1 + C2t,
y = C3 + C4 t, jos m = 0.
31. Olkoon f : 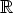 2
2 
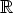 riittävän monta kertaa derivoituva kahden muuttujan funktio.
Laske alkuarvoprobleeman y' = f(x,y), y(x0) = y0 ratkaisun y(x) kolmannen asteen
Taylorin polynomi kehityskeskuksena x0. Laske myös neljännen asteen Taylorin polynomi
laskentaohjelman avulla.
riittävän monta kertaa derivoituva kahden muuttujan funktio.
Laske alkuarvoprobleeman y' = f(x,y), y(x0) = y0 ratkaisun y(x) kolmannen asteen
Taylorin polynomi kehityskeskuksena x0. Laske myös neljännen asteen Taylorin polynomi
laskentaohjelman avulla.
32. Laske alkuarvoprobleeman y' = x2 - y2, y(0) = 1 ratkaisun y(x) viidennen asteen origokeskinen Taylorin polynomi yhtälöä ratkaisematta. Muodosta tarvittavat funktion y derivaatat derivoimalla differentiaaliyhtälöä.
33. Laske alkuarvoprobleeman y'' = yy'- x2, y(0) = y'(0) = 1 ratkaisun viidennen asteen Maclaurinin polynomi yhtälöä ratkaisematta. Muodosta tarvittavat funktion y derivaatat derivoimalla differentiaaliyhtälöä.
34. Olkoon f : 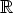 2
2 
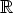 differentioituva funktio ja olkoon y differentiaaliyhtälön
y' = f(x, y) alkuehdon y(x0) = y0 toteuttava ratkaisu. Johda lauseke derivaatalle
y'' (x0 ).
differentioituva funktio ja olkoon y differentiaaliyhtälön
y' = f(x, y) alkuehdon y(x0) = y0 toteuttava ratkaisu. Johda lauseke derivaatalle
y'' (x0 ).
35. Määritä alkuarvoprobleeman xy' = x + y, y(1) = 1 ratkaisukäyrän kaarevuus alkuehtopisteessä.
36. Tutki, millaisia ratkaisuja on differentiaaliyhtälöllä y'(y(x)) = y(x).
37. Ratkaise integraaliyhtälö
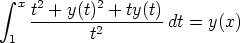
muodostamalla ensin puolittain derivoimalla differentiaaliyhtälö.
38. Ratkaise differentiaaliyhtälö yy''' = y'y'' sijoituksella u = y'/y.
39. Olkoon funktio P(x) derivoituva. Tee lineaariseen differentiaaliyhtälöön y'' + P (x)y' + Q(x)y = 0 sijoitus
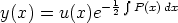
ja saata se muotoon u'' + I(x)u = 0. Mikä on funktion I(x) lauseke?
40. Olkoon funktio P(x) jatkuva. Kerro lineaarinen differentiaaliyhtälö y'' + P(x)y' + Q(x)y = 0 funktiolla
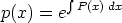
ja saata tulos muotoon
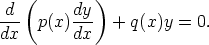
Millainen funktio on q(x)?
41. Funktio y olkoon jatkuva ja toteuttakoon integraaliyhtälön
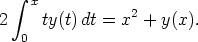
Määritä y käsinlaskulla. Tutki, miten laskentaohjelmaa voidaan hyödyntää tehtävän ratkaisemisessa.
42. Palauta Bernoulli’n differentiaaliyhtälö y' = A(x)y + B(x)yp lineaariseksi ensimmäisen
kertaluvun yhtälöksi sijoituksella z = y1-p. Ratkaise tällä tavoin seuraavat yhtälöt:
a) 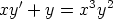
b) 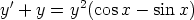
c) 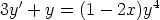
d) 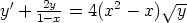
43. Riccati’n differentiaaliyhtälö on muotoa y' = A(x) + B(x)y + C(x)y2 ja
Bernoulli’n differentiaaliyhtälö muotoa y' = A(x)y + B(x)yp. Olkoon y
0(x) Riccati’n
yhtälön yksittäisratkaisu. Muunna Riccati’n yhtälö Bernoulli’n yhtälöksi sijoituksella
y(x) = y0 (x) + z(x). Muunna tällä tavoin seuraavat Riccati’n yhtälöt, kun annettuna
on yksittäisratkaisun periaatteellinen muoto. Ratkaise saamasi Bernoulli’n yhtälö
(tuntemattomana funktiona z(x)) sijoituksella u(x) = z(x)1-p. Mieti, miten laskentaohjelmaa
voidaan laskussa hyödyntää. Onnistuuko alkuperäisen yhtälön ratkaiseminen suoraan?
a) 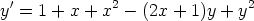 ,
,
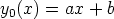
b) 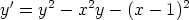 ,
,
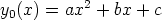
c) 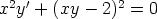 ,
,
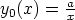
44. Muunna differentiaaliyhtälö x2y''' + 2(x2 -x)y'' + (x2 - 2x + 2)y' = x3 ottamalla uudeksi tuntemattomaksi funktioksi u(x) = y'(x)/x. Totea, että tällöin syntyy lineaarinen vakiokertoiminen yhtälö ja ratkaise se. Ratkaise tämän avulla alkuperäinen yhtälö.
45. Etsi kaikilla vakion a 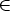
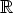 arvoilla integro-differentiaaliyhtälön
arvoilla integro-differentiaaliyhtälön
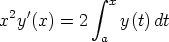
ratkaisu johtamalla ensin differentiaaliyhtälö funktiolle y.
46. Määritä differentiaaliyhtälön y'3 = y yleinen ratkaisu. Piirrä ratkaisukäyriä. Onko yhtälöllä erikoisratkaisuja? Onko olemassa alkuehtoa, joka ei määrää ratkaisua yksikäsitteisesti?
47. Ratkaise differentiaaliyhtälö y'2 = 4y. Onko yhtälöllä erikoisratkaisuja? Onko olemassa ehdot y(-1) = 1, y(2) = 1 toteuttavaa ratkaisua?
48. Onko alkuarvoprobleemalla a) y' = x2 - y2, y(0) = 0, b) y' = x2 - y2, y(0) = 1 olemassa yksikäsitteinen ratkaisu? Piirrä myönteisessä tapauksessa ratkaisufunktion kuvaaja origon ympäristössä jotakin menettelyä käyttäen.
49. Alkuarvoprobleeman y' = f(x,y), y(x0) = y0 ratkaisun olemassaolotodistuksessa käytetään Picardin – Lindelöfin menettelyä:
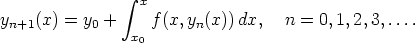
Etsi tätä käyttäen approksimaatioita alkuarvoprobleeman y' = xy, y(0) = 1 ratkaisulle. Valitse aloitusfunktioksi vakiofunktio y0(x) = 1. Vertaa tulosta tarkan ratkaisun Maclaurinin polynomiin.
50. Alkuarvoprobleeman y' = f(x,y), y(x0) = y0 ratkaisun olemassaolotodistuksessa käytetään Picardin – Lindelöfin menettelyä:
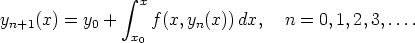
Tarkastellaan alkuarvoprobleemaa y' = f(x,y) = 2x + 5y, y(0) = 0. Osoita, että funktio f täyttää tasaisen Lipschitzin ehdon ja laske probleeman ratkaisulle Picardin – Lindelöfin menetelmän mukaiset approksimaatiot yk(x), k = 1, 2, 3, 4, kun valitaan y0 (x) = 0.
51. Alkuarvoprobleeman y' = f(x,y), y(x0) = y0 ratkaisun olemassaolotodistuksessa käytetään Picardin – Lindelöfin menettelyä:
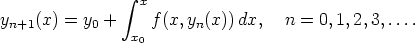
Laske tällä tavoin approksimoivia polynomeja alkuarvoprobleeman y' = x2 - y2, y(0) = 1 ratkaisulle.
52. Alkuarvoprobleeman y' = f(x,y), y(x0) = y0 ratkaisun olemassaolotodistuksessa käytetään Picardin – Lindelöfin menettelyä:
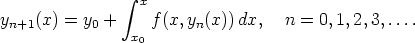
Approksimoi tällä tavoin alkuarvoprobleeman y'' + xy = 0, y(0) = 0, y'(0) = 1 ratkaisua. Differentiaaliyhtälö on ensin kirjoitettava normaaliryhmän muotoon Y ' = F(x,Y ), missä Y ja F ovat vektoriarvoisia funktioita. Laske funktiojonon alkupään termejä ja vertaa niiden antamaa approksimaatiota alkuarvoprobleeman tarkkaan ratkaisuun (joka on lausuttavissa Airyn funktioiden avulla).
53. Tutki seuraavien differentiaaliyhtälöiden tai alkuarvoprobleemoiden ratkaisemista
symbolisen tietokoneohjelman avulla:
a) 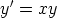
b) 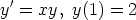
c) 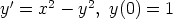
d) 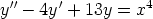
e) 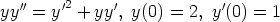
f) 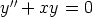
54. Ratkaise yhtälö y'' = f(y) laskentaohjelmalla. Mitä tarkoitetaan, kun sanotaan, että tällainen yhtälö aina voidaan ratkaista kahdella integroinnilla?
55. Määritä laskentaohjelmalla Besselin differentiaaliyhtälön x2y'' + xy' + (x2 - n2)y = 0 yleinen ratkaisu. Tässä n on parametri, joka voi saada minkä tahansa reaaliarvon. Kokeile ensin symbolilla n, ja anna sille tämän jälkeen kokonaislukuarvoja ja yksinkertaisia murtolukuarvoja. Ratkaisut ovat muotoa C1y1(x) + C2y2(x). Miten funktiot y1 ja y2 suhtautuvat toisiinsa parametrin n eri arvoilla? Millaisia ominaisuuksia niillä on? Rajoitu tarkastelemaan arvoja x > 0.
56. Osoita laskentaohjelmaa käyttäen, että differentiaaliyhtälön y' = x - y2 yleinen ratkaisu on
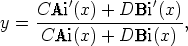
missä Ai ja Bi ovat Airyn funktiot; C ja D ovat vakioita. Huomaa, että integroimisvakioita on oleellisesti yksi: lauseke voidaan supistaa joko C:llä tai D:llä. Piirrä ratkaisukäyriä ja tutki, millaisessa erikoisasemassa ovat arvoja C = 0 tai D = 0 vastaavat ratkaisut.
57. Ratkaise seuraavat yhtälöryhmät laskentaohjelmalla ja pyri saattamaan vastaus
mahdollisimman yksinkertaiseen muotoon. Tutki, mitkä vakion a 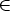
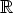 arvot ovat
poikkeusasemassa, ts. yleisessä tapauksessa saatu ratkaisu ei ole pätevä näillä arvoilla. Tutki
myös, toteuttavatko saamasi ratkaisut yhtälöparin.
arvot ovat
poikkeusasemassa, ts. yleisessä tapauksessa saatu ratkaisu ei ole pätevä näillä arvoilla. Tutki
myös, toteuttavatko saamasi ratkaisut yhtälöparin.
a) 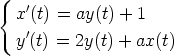
b) 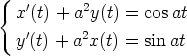
58. Ratkaise laskentaohjelmalla numeerisesti ja symbolisesti alkuarvotehtävä y' = y2 - cos x, y(0) = 1. Piirrä kummankin ratkaisun kuvaaja ja laske y(1.5). Onko yhtälö ratkaistavissa alkeisfunktioiden avulla?
59. Ratkaise laskentaohjelmalla alkuarvoprobleema
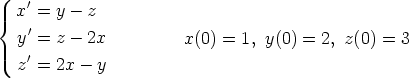
numeerisesti ja symbolisesti. Piirrä kummassakin tapauksessa saatujen ratkaisukäyrien kuvaajat välillä [0, 20] ja laske ratkaisufunktioiden arvot pisteessä t = 20. Millä tarkkuudella numeerinen ja symbolinen tulos on sama?
60. Ratkaise laskentaohjelmalla numeerisesti alkuarvoprobleema y''' = |y|3 - y2, y(0) = 1, y'(0) = -1, y''(0) = 0 antamalla syötteeksi yhtälö a) ylläolevassa muodossa, b) normaaliryhmänä. Millä välillä ratkaisu on olemassa?
61. Ratkaise laskentaohjelmalla numeerisesti alkuarvoprobleema x'' + y = sin t, y'' + x = cos t, x(0) = 0, x'(0) = 1, y(0) = 1, y'(0) = 0. Tarkastele ratkaisuja välillä [0, 30]. Tutki ratkaisun herkkyyttä alkuarvojen muutoksille käyttämällä hieman poikkeavaa alkuehtoa, esimerkiksi x(0) = 0, x'(0) = 0.9999, y(0) = 1.0001, y'(0) = 0. Voidaanko yhtälöryhmä ratkaista tarkasti?
62. Etsi separoimalla seuraavien differentiaaliyhtälöiden yleiset ratkaisut. Piirrä
ratkaisukäyriä.
a) 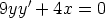
b) 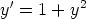
63. Ratkaise separoimalla seuraavat alkuarvotehtävät.
a) 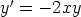 ,
,
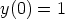
b) 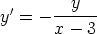 ,
,
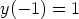
c) 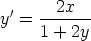 ,
,
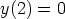
d) 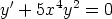 ,
,
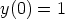
e) 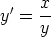 ,
,
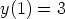
64. Määritä seuraavien differentiaaliyhtälöiden yleiset ratkaisut. Piirrä ratkaisukäyrien
kuvaajia. Valitse jokin alkuehto, joka antaa muun kuin vakioratkaisun, ja tutki, missä alueessa
vastaava ratkaisu on määritelty. Voidaanko alkuehto antaa missä tahansa pisteessä?
a) 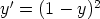
b) 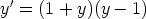
c) 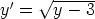
65. Määritä seuraavien differentiaaliyhtälöiden yleiset ratkaisut. Piirrä ratkaisukäyrien
kuvaajia. Valitse jokin alkuehto, joka antaa muun kuin vakioratkaisun, ja tutki, missä alueessa
vastaava ratkaisu on määritelty. Voidaanko alkuehto antaa missä tahansa pisteessä?
a) 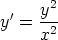
b) 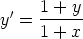
c) 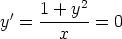
d) 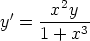
e) 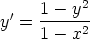
66. Ratkaise seuraavat alkuarvoprobleemat. Voidaanko separointia ongelmitta soveltaa?
a) 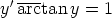 ,
,
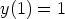
b) 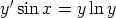 ,
,
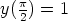
c) 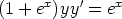 ,
,
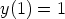
d) 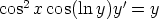 ,
,
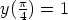
67. Ratkaise seuraavat alkuarvoprobleemat.
a) 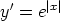 ,
,
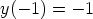
b) 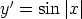 ,
,
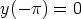
68. Etsi ne differentiaaliyhtälön y' = 2x|y - 1| ratkaisukäyrät, jotka sivuavat x-akselia.
69. Ratkaise seuraavat differentiaaliyhtälöt sopivaa sijoitusta käyttäen. Piirrä ratkaisukäyrien
kuvaajia. Onko yhtälöillä ratkaisuja, joiden kuvaajat ovat suoria?
a) 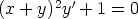
b) 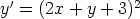
c) 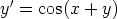
70. Ratkaise seuraavat differentiaaliyhtälöt ja piirrä ratkaisukäyrien kuvaajia.
a) 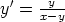
b) 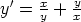
c) 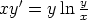
71. Ratkaise seuraavat differentiaaliyhtälöt. Piirrä ratkaisujen kuvaajia.
a) 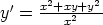
b) 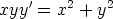
c) 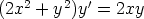
72. Ratkaise differentiaaliyhtälö 1 + y2 + xyy' = 0 sopivalla sijoituksella.
73. Ratkaise alkuarvoprobleema y' = 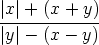 , y(2) = 0.
, y(2) = 0.
74. Piirrä differentiaaliyhtälön xy' = x + y suuntakenttä. Etsi yhtälön ratkaisu. Piirrä suuntakenttään alkuehdon y(1) = 1 toteuttava ratkaisukäyrä.
75. Osoita, että yhtälön
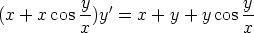
yleinen ratkaisu voidaan esittää parametrimuodossa seuraavasti: x = Cet+sin t, y = Ctet+sin t.
Etsi tämä ratkaisu sopivaa sijoitusta ja separointia käyttäen. Piirrä ratkaisukäyrä, joka
toteuttaa alkuehdon y(1) = 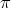 /2.
/2.
76. Ratkaise differentiaaliyhtälö 2xyy'- y2 + x2 = 0 sopivalla sijoituksella. Mitä mahdetaan tarkoittaa, kun yhtälöä kutsutaan erään ympyräparven differentiaaliyhtälöksi?
77. Olkoon funktio f : 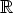

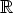 kaikkialla jatkuvasti derivoituva ja
kaikkialla jatkuvasti derivoituva ja 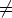 0. Etsi yhtälön
0. Etsi yhtälön
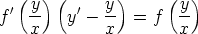
yleinen integraali.
78. Ratkaise alkuarvoprobleema eyy' = x + ey - 1, y(0) = a sijoituksella u = x + ey. Mikä ehto
vakion a on täytettävä, jotta ratkaisufunktio olisi määritelty kaikilla arvoilla x 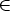
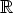 ? Jos a ei
täytä tätä ehtoa, funktiolla on singulariteetti jossakin pisteessä. Millaisesta yhtälöstä tämä
saadaan? Millä välillä singulariteetti sijaitsee?
? Jos a ei
täytä tätä ehtoa, funktiolla on singulariteetti jossakin pisteessä. Millaisesta yhtälöstä tämä
saadaan? Millä välillä singulariteetti sijaitsee?
79. Tutki seuraavien yhtälöiden muuntumista muuttujien vaihdossa x = ta, y = ub.
Valitse vakioille a ja b arvot siten, että yhtälöistä tulee tasa-asteisia ja ratkaise ne.
a) 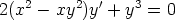
b) 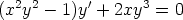
80. Muotoa y' = f(L1/L2) oleva differentiaaliyhtälö, missä L1 = a1x + b1y + c1 ja
L2 = a2 x + b2 y + c2, voidaan palauttaa separoituvaan sijoituksella x = u + x0, y = v + y0, missä
(x0 , y0 ) on suorien L1 = 0 ja L2 = 0 leikkauspiste. Ratkaise tällä tavoin seuraavat
differentiaaliyhtälöt.
a) 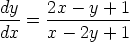
b) 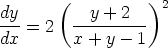
81. Ratkaise seuraavat differentiaaliyhtälöt.
a) 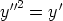
b) 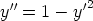
c) 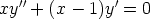
d) 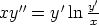
82. Muodosta seuraavia differentiaaliyhtälöitä vastaavat normaaliryhmät. Ratkaise yhtälöt
näiden avulla käsinlaskulla. Ratkaise yhtälöt laskentaohjelmalla lähtemällä alkuperäisestä
yhtälöstä ja toisaalta normaaliryhmästä. Tutki, ovatko eri tavoin saadut ratkaisut samoja.
a) 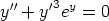
b) 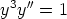
c) 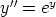
d) 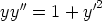
e) 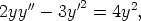
f) 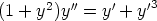
83. Muodosta seuraavia differentiaaliyhtälöitä vastaavat normaaliryhmät. Ratkaise yhtälöt
näiden avulla käsinlaskulla. Ratkaise yhtälöt laskentaohjelmalla lähtemällä alkuperäisestä
yhtälöstä ja toisaalta normaaliryhmästä. Tutki, ovatko eri tavoin saadut ratkaisut samoja.
a) 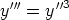
b) 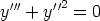
c) 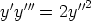
d) 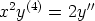
e) 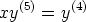
84. Osoita differentiaaliyhtälöt
a) 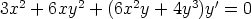
b) 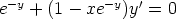
c) 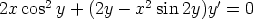
eksakteiksi ja ratkaise ne. Piirrä suuntakentät ja ratkaisukäyriä.
85. Totea, että differentiaaliyhtälöllä (3x2 - y2 - 3)y' + 2xy = 0 on integroiva tekijä y2. Ratkaise yhtälö ja piirrä sen ratkaisukäyriä.
86. Totea, että differentiaaliyhtälö x2y'- 2xy + 3 = 0 ei ole eksakti, mutta siitä voidaan saada eksakti kertomalla se muotoa F(x) olevalla integroivalla tekijällä. Ratkaise yhtälö tällä tavalla. Piirrä suuntakenttä ja ratkaisukäyriä.
87. Differentiaaliyhtälöllä (2xy - y2 - y)dx + (2xy - x2 - x)dy = 0 on muotoa F(x + y) oleva integroiva tekijä. Ratkaise yhtälö tämän perusteella. Piirrä suuntakenttä ja ratkaisukäyriä.
88. Osoita, että jos differentiaaliyhtälössä
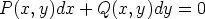
(P y - Qx )/Q on pelkästään muuttujan x funktio, niin yhtälöllä on muotoa F(x) oleva
integroiva tekijä, ja jos (Py - Qx)/P on pelkästään muuttujan y funktio, niin yhtälöllä on
muotoa F (y) oleva integroiva tekijä. (Alaindeksit tarkoittavat osittaisderivaattoja.) Ratkaise
tällä menettelyllä seuraavat differentiaaliyhtälöt.
a) 
b) 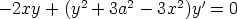
c) 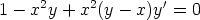
d) 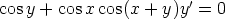
89. Onko differentiaaliyhtälö y'' + x(y'- y'') = y + 1 a) lineaarinen, b) homogeeninen?
90. Olkoot u(x) ja v(x) jatkuvasti derivoituvia funktioita tarkasteluvälillä ja olkoon
tällä välillä u(x)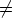 0. Etsi ensimmäisen kertaluvun lineaarinen differentiaaliyhtälö,
jonka yleinen ratkaisu on y = Cu(x) + v(x). Ratkaise saamasi differentiaaliyhtälö
laskentaohjelmalla.
0. Etsi ensimmäisen kertaluvun lineaarinen differentiaaliyhtälö,
jonka yleinen ratkaisu on y = Cu(x) + v(x). Ratkaise saamasi differentiaaliyhtälö
laskentaohjelmalla.
91. Olkoon y1(x) = x2 ja y 2(x) = x|x|. Osoita, että funktiot ovat lineaarisesti riippumattomia ja että niiden Wronskin determinantti on = 0. Onko mahdollista muodostaa toisen kertaluvun lineaarinen ja homogeeninen differentiaaliyhtälö, jonka ratkaisuja em. funktiot ovat?
92. Osoita, että eksponenttifunktio ja logaritmifunktio ovat differentiaaliyhtälön
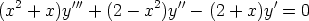
ratkaisuja. Mikä on yhtälön yleinen ratkaisu?
93. Osoita, että differentiaaliyhtälöllä
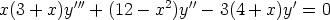
on ratkaisuina y = ex ja y = 1/x2. Mikä on differentiaaliyhtälön yleinen ratkaisu?
94. Muodosta toisen kertaluvun homogeeninen lineaarinen differentiaaliyhtälö, jolla on
yksityisratkaisuina kahdesti derivoituvat funktiot u(x) ja v(x), joiden Wronskin determinantti
on 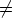 0.
0.
95. Lineaarisella homogeenisella toisen kertaluvun differentiaaliyhtälöllä on yksityisratkaisuina u(x) = x ja v(x) = cos x. Muodosta yhtälö ja määritä sen ratkaisuista se, jonka kuvaaja sivuaa suoraa y = x + 1 origossa.
96. Osoita, että eksponenttifunktio ja logaritmifunktio ovat differentiaaliyhtälöä
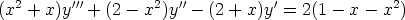
vastaavan homogeeniyhtälön ratkaisuja. Totea, että epähomogeenisella yhtälöllä on ratkaisuna eräs toisen asteen polynomi. Mikä on yhtälön yleinen ratkaisu?
97. Differentiaaliyhtälöllä
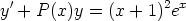
on ratkaisuna y = (x2 - 1)ex. Määritä P(x) ja yhtälön yleinen ratkaisu. Etsi alkuehdon y(0) = 0 toteuttava yksityisratkaisu. Millä välillä tämä yksityisratkaisu on määritelty? Miten tehtävä voidaan ratkaista laskentaohjelmalla?
98. Funktiot u(x) ja v(x) ovat yhtälön y' + a(x)y = 0 ratkaisuja, funktiot u(x) + ex ja v(x) - 1 yhtälön y' + a(x)y + b(x) = 0 ratkaisuja. Määritä funktiot a(x) ja b(x) sekä se jälkimmäisen yhtälön ratkaisu, jonka kuvaaja kulkee origon kautta.
99. Tutki, millaisia kohdassa x = 0 annettuja alkuehtoja arvoa n = 1 vastaavaan Besselin differentiaaliyhtälöön x2y'' + xy' + (x2 - 1)y = 0 voidaan liittää. Mikä on tilanne, jos ehdot annetaan kohdassa x = 1?
100. Ratkaise seuraavat differentiaaliyhtälöt sekä käsinlaskulla että laskentaohjelmalla. Vertaa
tuloksia.
a) 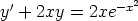
b) 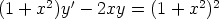
c) 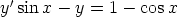
101. Ratkaise seuraavat alkuarvoprobleemat a) käsinlaskulla, b) laskentaohjelmalla
symbolisesti, c) laskentaohjelmalla numeerisesti. Vertaa tuloksia. Piirrä kuvaajat.
a) 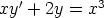 ,
,
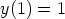
b) 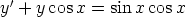 ,
,
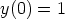
c) 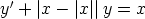 ,
,
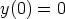
102. Ratkaise alkuarvoprobleema
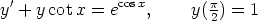
laskentaohjelmalla sekä symbolisesti että numeerisesti. Piirrä ratkaisukäyrä. Millä välillä tämä on määritelty?
103. Olkoon funktio r(x) jatkuva ja olkoon y(x) alkuarvoprobleeman y' + 3x2y = r(x), y(0) = 0 ratkaisu. Mitä arvoja y(-1) ja y(1) voivat saada, kun r(x) < x2?
104. Määritä differentiaaliyhtälön y' = |y - x| yleinen ratkaisu. Piirrä suuntakenttä ja ratkaisukäyriä. Määritä alkuehdon y(1) = 2 toteuttava yksittäisratkaisu.
105. Ratkaise seuraavat differentiaaliyhtälöt, kun tiedetään että yhtenä yksityisratkaisuna on
polynomi. Kokeile myös ratkaisemista laskentaohjelmalla ja vertaa tuloksia. Tutki, onko
mahdollista antaa alkuehto origossa.
a) 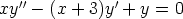
b) 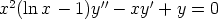
c) 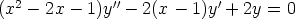
106. Osoita, että differentiaaliyhtälöllä y'' + (tan x- 2 cot x)y' + 2(cot 2x)y = 0 on ratkaisuna sinx ja etsi yhtälön yleinen ratkaisu.
107. Osoita, että differentiaaliyhtälöllä (x- 2)y''- (4x- 7)y' + (4x- 6)y = 0 on muotoa ekx oleva ratkaisu ja etsi yhtälön yleinen ratkaisu.
108. Totea, että seuraavissa differentiaaliyhtälöissä kerroinfunktioiden summa on = 1 ja käytä
tätä tietoa yhden yksityisratkaisun löytämiseen. Etsi yhtälöiden yleiset ratkaisut käsinlaskulla.
Kokeile myös laskentaohjelman käyttöä.
a) 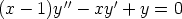
b) 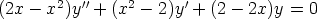
c) 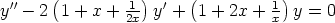
109. Etsi laskentaohjelmalla Airyn differentiaaliyhtälön y''- xy = 0 yleinen ratkaisu. Etsi yksityisratkaisut, kun alkuehtona on a) y(0) = 0, y'(0) = 1, b) y(0) = 1, y'(0) = 0. Piirrä ratkaisujen kuvaajat samaan kuvioon. Tarkastele erityisesti negatiivisia muuttujan arvoja. Miten ratkaisufunktioiden nollakohdat näyttävät suhtautuvan toisiinsa?
110. Differentiaaliyhtälöllä y'' + y = 0 on yksittäisratkaisuina sin x ja cos x. Etsi yleisellä
vakioiden varioinnilla differentiaaliyhtälön y'' + y = 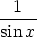 yleinen ratkaisu.
yleinen ratkaisu.
111. Etsi differentiaaliyhtälön y'' + x(y'- y'') = y + 1 yksittäisratkaisu, kun alkuehtona on a) y(0) = y'(0) = 0, b) y(1) = y'(1) = 0, c) y(1) = 0, y'(1) = 1.
112. Etsi differentiaaliyhtälön y'' + y' tan x = x cos x yleinen ratkaisu.
113. Etsi differentiaaliyhtälön (x - 1)y''- xy' + y = x - 1 yleinen ratkaisu ja alkuehdon y(2) = 1, y'(2) = 0 toteuttava yksittäisratkaisu.
114. Sovella yleistä vakioiden variointia yhtälön y'' + ay' + by = R(x) yksityisratkaisun etsimiseen, kun a2 - 4b on a) > 0, b) = 0, c) < 0.
115. Pidetään tunnettuna, että homogeeniyhtälön y'' + 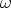 2y = 0 ratkaisut ovat y
1(x) = sin
2y = 0 ratkaisut ovat y
1(x) = sin 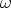 x,
y2 (x) = cos
x,
y2 (x) = cos 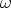 x. Sovella vakioiden variointia yhtälön y'' +
x. Sovella vakioiden variointia yhtälön y'' + 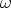 2y = A sin
2y = A sin 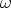 x + B cos
x + B cos 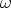 x
yksityisratkaisun etsimiseen.
x
yksityisratkaisun etsimiseen.
116. Etsi seuraavien yhtälöiden yleiset ratkaisut laskemalla käsin.
a) 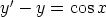
b) 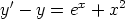
117. Ratkaise alkuarvoprobleemat laskemalla käsin.
a) 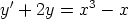 ,
,
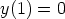
b) 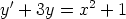 ,
,
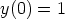
c) 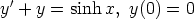
118. Muodosta kaikilla vakioiden a, b arvoilla vakiokertoimisen yhtälön y'' + ay' + by = 0 perusratkaisut. Laske perusratkaisujen Wronskin determinantti ja saata se mahdollisimman yksinkertaiseen muotoon.
119. Olkoon a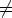 0. Määritä origossa annettu alkuehto, jolla yhtälön y' + ay = A sin
0. Määritä origossa annettu alkuehto, jolla yhtälön y' + ay = A sin 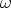 x
ratkaisu on jaksollinen. Määritä tämän amplitudi.
x
ratkaisu on jaksollinen. Määritä tämän amplitudi.
120. Etsi seuraavien yhtälöiden yleiset ratkaisut käsin laskemalla.
a) 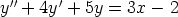
b) 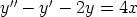
c) 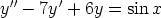
d) 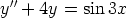
e) 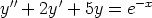
121. Etsi seuraavien yhtälöiden yleiset ratkaisut käsin laskemalla.
a) 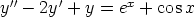
b) 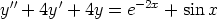
c) 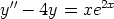
122. Etsi käsin laskemalla yleinen ratkaisu differentiaaliyhtälölle y''- 6y' + 9y = e3x/x2.
123. Ratkaise seuraavat alkuarvoprobleemat
a) 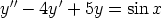 ,
,
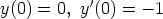
b) 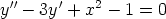 ,
,
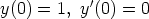
c) 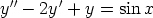 ,
,
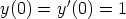
124. Ratkaise reuna-arvoprobleema y''- 5y' + 6y = ex, y(0) = y(1) = 0.
125. Määritä sellainen alkuehto, että yhtälön y'' + 5y' + 6y = x yksittäisratkaisu on polynomi.
126. Ratkaise alkuarvoprobleema y'' + y = 2 sin x, y(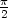 ) = 1, y'(
) = 1, y'(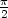 ) =
) = 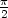 .
.
127. Olkoot a ja b mitä tahansa reaalilukuja. Tutki, mitä laskentaohjelma antaa seuraavien
differentiaaliyhtälöiden yleisiksi ratkaisuiksi. Ovatko saadut ratkaisut päteviä kaikilla vakioiden
arvoilla?
a) 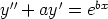
b) 
c) 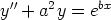
d) 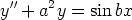
e) 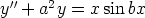
f) 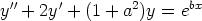
128. Ratkaise sekä käsin laskemalla että laskentaohjelmalla differentiaaliyhtälö
y'' + 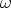 2 y = A sin
2 y = A sin 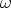 x + B cos
x + B cos 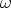 x.
x.
129. Olkoon h(x) lineaarista vakiokertoimista differentiaaliyhtälöä y'' + ay' + by = R(x) vastaavan homogeeniyhtälön ratkaisu, joka toteuttaa alkuehdot h(0) = 0, h'(0) = 1. Osoita, että
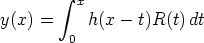
on epähomogeenisen yhtälön yksityisratkaisu, jolle y(0) = y'(0) = 0. Ratkaise tällä menettelyllä alkuarvoprobleema y'' + y = tan x, y(0) = y'(0) = 0. Tarkista sijoittamalla, että tulos todella on alkuarvoprobleeman ratkaisu.
130. Määritä ne reaaliset parametrin a arvot, joilla yhtälöillä
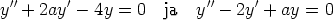
on yhteinen ei-triviaali (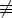 0) ratkaisu. Määritä kussakin tapauksessa yhteinen ratkaisu. Tutki
tehtävän ratkaisemista sekä laskentaohjelmalla että käsin laskemalla.
0) ratkaisu. Määritä kussakin tapauksessa yhteinen ratkaisu. Tutki
tehtävän ratkaisemista sekä laskentaohjelmalla että käsin laskemalla.
131. Ratkaise seuraavat differentiaaliyhtälöt.
a) 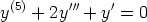
b) 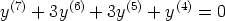
c) 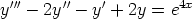
d) 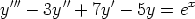
e) 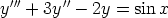
132. Ratkaise seuraavat differentiaaliyhtälöt.
a) 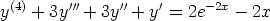
b) 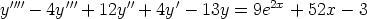
c) 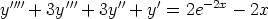
133. Ratkaise seuraavat alkuarvoprobleemat.
a) 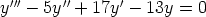 ,
,
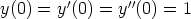
b) 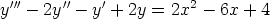 ,
,
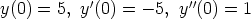
c) 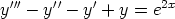 ,
,
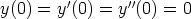
134. Olkoon a 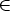
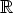 . Etsi laskentaohjelmaa käyttäen seuraavien differentiaaliyhtälöiden yleiset
ratkaisut ja esitä nämä kaikissa tapauksissa reaalisessa muodossa. Tutki, mitkä vakion a arvot
ovat poikkeuksellisia: ratkaisun muoto on erilainen. Hae ratkaisu erikseen näissä tapauksissa.
. Etsi laskentaohjelmaa käyttäen seuraavien differentiaaliyhtälöiden yleiset
ratkaisut ja esitä nämä kaikissa tapauksissa reaalisessa muodossa. Tutki, mitkä vakion a arvot
ovat poikkeuksellisia: ratkaisun muoto on erilainen. Hae ratkaisu erikseen näissä tapauksissa.
a) 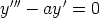
b) 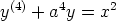
c) 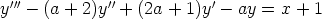
135. Etsi kaikki differentiaaliyhtälön y''' + y'' + 2y' + 2y = 0 jaksolliset ratkaisut.
136. Muunna Eulerin differentiaaliyhtälö
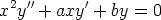
sijoituksella t = ln |x| vakiokertoimiseksi lineaariyhtälöksi. Sovella tulosta yhtälöön
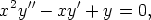
ratkaise saatu vakiokertoiminen yhtälö ja muodosta tämän avulla alkuperäisen yhtälön yleinen ratkaisu.
137. Ratkaise seuraavat differentiaaliyhtälöt käyttämällä muotoa y = xr olevaa yritettä.
a) 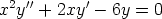
b) 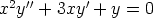
c) 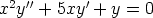
d) 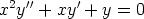
e) 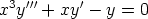
138. Ratkaise differentiaaliyhtälö x2y''- 2xy' + 2y = x2 sin x yritteellä y = xr ja vakioiden
varioinnilla. Etsi alkuehtoa y(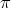 ) =
) = 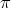 , y'(
, y'(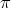 ) = 0 vastaava yksittäisratkaisu.
) = 0 vastaava yksittäisratkaisu.
139. Etsi seuraavien differentiaaliyhtälöiden yleiset ratkaisut.
a) 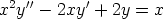
b) 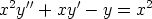
c) 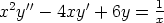
140. Olkoot p ja q reaalilukuja. Ratkaise laskentaohjelmalla kaikissa tapauksissa differentiaaliyhtälö x2y'' + (2p + 1)xy' + qy = 0. Esitä vastaus reaalisessa muodossa.
141. Ratkaise differentiaaliyhtälöt
a) 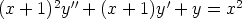
b) 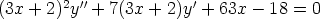
142. Tutki, mitkä vakion a 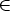
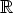 arvot johtavat muotoa xp ln x, p
arvot johtavat muotoa xp ln x, p 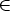
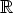 , olevien funktioiden
esiintymiseen differentiaaliyhtälön x3y''' + 2x2y''- 4xy' + ay = 0 yleisessä ratkaisussa.
, olevien funktioiden
esiintymiseen differentiaaliyhtälön x3y''' + 2x2y''- 4xy' + ay = 0 yleisessä ratkaisussa.
143. Seuraavissa differentiaaliyhtälöryhmissä riippumattomana muuttujana on x ja
tuntemattomat funktiot ovat y(x) ja z(x). Palauta ryhmät yhdeksi differentiaaliyhtälöksi
eliminoimalla toinen tuntematon funktio. Etsi tällä tavoin ryhmien ratkaisut. Ratkaise
yhtälöryhmät myös suoraan laskentaohjelmalla. Vertaa eri tavoin saatuja tuloksia.
a) 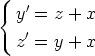
b) 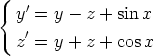
c) 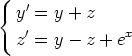
d) 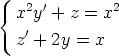
144. Ratkaise seuraavat alkuarvoprobleemat sekä käsin laskelmalla että laskentaohjelmalla.
Vertaa tuloksia.
a) 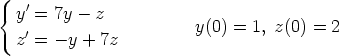
b) 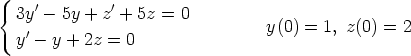
c) 
d) 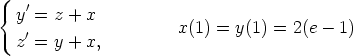
145. Olkoot x, y ja z muuttujan t funktioita. Etsi differentiaaliyhtälöryhmän x' + y = y' + z = z' + x = 0 yleinen ratkaisu sekä alkuehdon x(0) = y(0) = z(0) = 1 toteuttava yksittäisratkaisu. Ratkaise tehtävä myös laskentaohjelmalla ja pyri saattamaan ratkaisu mahdollisimman yksinkertaiseen muotoon.
146. Olkoot x ja y muuttujan t funktioita. Tutki piirtämällä seuraavien differentiaaliyhtälöryhmien
ratkaisukäyriä faasiavaruudessa. Määritä faasitasokäyrien yhtälöt.
a) 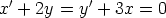
b) 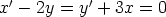
147. Olkoot x(t), y(t), z(t) ja u(t) tuntemattomia funktioita, joille pätee x' = y, y' = z, z' = u, u' = x. Määritä funktiot. Tutki piirtämällä ratkaisukäyriä faasiavarudessa. Etsi jokin faasiavaruudessa rajoitettu ratkaisukäyrä ja piirrä tämän projektiot faasiavaruuden koordinaattitasoille.
148. Olkoot x(t), y(t) ja z(t) tuntemattomat funktiot. Ratkaise differentiaaliyhtälöryhmä
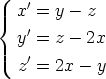
alkuehdolla x(0) = 1, y(0) = 2, z(0) = 3. Laske käsin ja tarkasta tulos laskentaohjelmalla.
149. Ratkaise laskentaohjelmalla differentiaaliyhtälöryhmä x' = y/t, y' = z/t, z' = x/t, missä
tuntemattomat funktiot ovat x(t), y(t) ja z(t). Tutki ratkaisukäyrän käyttäytymistä
xyz-avaruudessa, kun t 
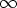 . Onko mahdollista löytää alkuehto, jolla käyrä lähestyisi
origoa?
. Onko mahdollista löytää alkuehto, jolla käyrä lähestyisi
origoa?
150. Olkoot x(t) ja y(t) tuntemattomat funktiot. Etsi yleinen ratkaisu seuraavalle differentiaaliyhtälöryhmälle sekä käsin laskemalla että laskentaohjelmalla.
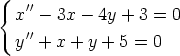
151. Johda välttämätön ja riittävä ehto sille, että differentiaaliyhtälöryhmän
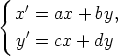
ratkaisussa esiintyy trigonometrisia funktioita. Onko ehto bc < 0 a) välttämätön, b) riittävä?
152. Kirjoita seuraavat differentiaaliyhtälöryhmät matriisimuotoon. Ratkaise ryhmät
laskentaohjelmalla. Määritä kerroinmatriisin ominaisarvot. Mikä yhteys näillä näyttäisi olevan?
a) 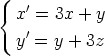
b) 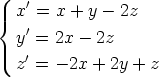
c) 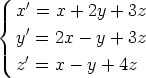
d) 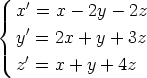
153. Ratkaise origokeskisen potenssisarjan avulla differentiaaliyhtälö (1 + x2)y'- 2xy = (1 + x2)2.
154. Etsi differentiaaliyhtälön y''- 2y' + y = 0 yleinen ratkaisu origokeskisen potenssisarjan muodossa. Ratkaise differentiaaliyhtälö myös alkeisfunktioiden avulla. Muodosta ratkaisufunktion Maclaurinin sarja. Onko tämä sama kuin edellä saatu sarjaratkaisu?
155. Etsi potenssisarjamuodossa ratkaisu alkuarvoprobleemalle y''- 2xy' + 2y = 0, y(0) = 1, y'(0) = 0. Määritä sarjan suppenemissäde.
156. Etsi differentiaaliyhtälön y'' = y yleinen ratkaisu origokeskisten potenssisarjojen avulla.
157. Etsi origokeskinen sarjaratkaisu Legendren differentiaaliyhtälölle
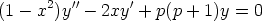
arvolla p = 2. Totea, että yhtälöllä on yksityisratkaisuna polynomi.
158. Etsi alkuarvoprobleemalle y' = x2 - y2, y(0) =  potenssisarjaratkaisu. Tutki sarjan
suppenemissädettä numeerisesti ja piirrä saadun sarjaratkaisun kuvaaja.
potenssisarjaratkaisu. Tutki sarjan
suppenemissädettä numeerisesti ja piirrä saadun sarjaratkaisun kuvaaja.
159. Etsi differentiaaliyhtälölle y' = x2 - y2 yksittäisratkaisu potenssisarjamuodossa, kun alkuehtona on a) y(0) = 0, b) y(0) = 1. Piirrä laskemasi osasumman kuvaaja. Ratkaise sama alkuarvoprobleema myös numeerisesti ja piirrä saadun numeerisen ratkaisun kuvaaja. Vertaa tuloksia. Laske approksimaatioita alkuehtoja vastaavien potenssisarjojen suppenemissäteille. Riippuuko suppenemissäde alkuehdosta? Onko mahdollista arvioida suppenemissädettä kuvaajien perusteella?
160. Ratkaise numeerisesti Eulerin menetelmällä alkuarvoprobleemat a) y' = y, y(0) = 1, b) y' = -y, y(0) = 1. Käytä askelpituudeksia h = 0.2 ja h = 0.5. Valitse tarkasteluväliksi [0, 5]. Vertaa tulosta tarkkaan ratkaisuun. Miten numeerisen ratkaisun virheen käy muuttujan kasvaessa? Millä tavalla a- ja b-kohta ovat tarkkuuden suhteen erilaisia?
161. Ratkaise numeerisesti Eulerin menetelmällä alkuarvoprobleema y' = 2xy + 1, y(0) = 1. Käytä askelpituuksia a) h = 0.2, b) h = 0.02. Piirrä ratkaisukäyrät välillä [-2, 1]. Muodosta myös yhtälön tarkka ratkaisu.
162. Ratkaise numeerisesti alkuarvoprobleema y' = |y2 - 1|, y(0) = -0.9. Käytä askelpituutta h = 0.5 ja vertaa eri menetelmiä. Tarkastele väliä [0, 7]. Laske myös tarkka ratkaisu.
163. Differentiaaliyhtälö
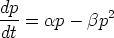
esittää erästä populaatiomallia; tässä p on populaation koko ja 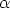 ,
, 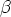 > 0 ovat vakioita.
Olkoon
> 0 ovat vakioita.
Olkoon 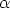 =
= 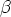 = 10 ja alkuehtona p(0) = 0.1. Muodosta Eulerin menetelmän mukainen
iteraatiokaava differentiaaliyhtälön numeerista ratkaisemista varten. Ratkaise yhtälö
käyttäen askelpituuksia h = 0.30, h = 0.25, h = 0.20, h = 0.15 ja h = 0.10. Kokeile
myös parannettua Eulerin menetelmää, Rungen – Kuttan ja Adamsin – Bashforthin
menetelmää.
= 10 ja alkuehtona p(0) = 0.1. Muodosta Eulerin menetelmän mukainen
iteraatiokaava differentiaaliyhtälön numeerista ratkaisemista varten. Ratkaise yhtälö
käyttäen askelpituuksia h = 0.30, h = 0.25, h = 0.20, h = 0.15 ja h = 0.10. Kokeile
myös parannettua Eulerin menetelmää, Rungen – Kuttan ja Adamsin – Bashforthin
menetelmää.
164. Tutki alkuarvoprobleeman y' = 2xy, y(0) = 1 numeerista ratkaisemista eri menetelmillä. Laske y(5). Käytä askelpituuksia h = 0.2 ja h = 0.5. Vertaa eri menetelmien antamia tuloksia ja selitä syntyneet erot.
165. Kirjoita differentiaaliyhtälöä y'' + xy' + y = 0 vastaava ensimmäisen kertaluvun normaaliryhmä ja muodosta tämän perusteella Eulerin menetelmän mukaiset numeeriset ratkaisukaavat, kun alkuehdot ovat y(0) = 1, y'(0) = 2.
166. Ratkaise numeerisesti eri menetelmillä alkuarvoprobleema y''' + 3y''- 2y = sin x, y(1) = 0.659804, y'(1) = -1.04984, y''(1) = 1.36261. Käytä askelpituuksia h = 0.1 ja h = 0.05. Valitse tarkasteluväliksi [1, 10]. Piirrä kuviot ja vertaa tuloksia. Mitä tapahtuu, jos ratkaisuja tarkastellaan pidemmällä välillä [1, 30]? Miksi? Muodosta ilmiön selittämiseksi yhtälön yleinen ratkaisu.
167. Differentiaaliyhtälöryhmä
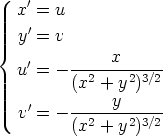
kuvaa planeetan liikettä kiinteän auringon ympäri ajan funktiona. Planeetan paikkakoordinaatit ovat x ja y, nopeuden komponentit u ja v. Ratkaise yhtälöryhmä numeerisesti eri menetelmillä eri alkuehtoja ja askelpituuksia käyttäen ja vertaa tuloksia. Esimerkiksi sopivasta alkuehdosta kelpaa x(0) = 0, y(0) = 1, u(0) = 0.5, v(0) = 0.5 ja sopivasta askelpituudesta h = 0.01. Kokeile kuitenkin muitakin.
168. Piirrä alkuarvotehtävän y' = (1 + x)y + 1 - 3x + x2, y(0) = 0.06 ratkaisukäyrät käyttäen sekä Eulerin että Rungen–Kuttan menetelmiä. Käytä askelpituutta h = 0.04. Voidaanko tämän perusteella olla varmoja ratkaisukäyrien kvalitatiivisesta käyttäytymisestä?
169. Tutki differentiaaliyhtälöryhmän
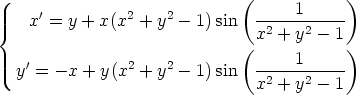
ratkaisukäyriä faasitasossa numeerisesti. Millaisia käyrät ovat? Millaisia käyriä (attraktoreja) ne lähestyvät?
170. Piirrä Rungen–Kuttan menetelmällä alkuarvoprobleeman y' = x-y2, y(0) = 0 ratkaisu
välillä x 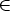 [0, 300]. Käytä askelpituutta h = 0.1. Havaintosi? Puolita askelpituus ja piirrä
kuvaaja uudelleen. Entä jos tällä puolitetulla askelpituudella piirrettäisiinkin ratkaisu välillä
x
[0, 300]. Käytä askelpituutta h = 0.1. Havaintosi? Puolita askelpituus ja piirrä
kuvaaja uudelleen. Entä jos tällä puolitetulla askelpituudella piirrettäisiinkin ratkaisu välillä
x 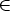 [0, 1000]? Mikä voisi olla selityksenä havaituille ilmiöille?
[0, 1000]? Mikä voisi olla selityksenä havaituille ilmiöille?
171. Tutki alkuarvoprobleeman y' = x - y2, y(0) = 0 numeerista ratkaisua eri menetelmillä välillä [0, 1000]. Käytä askelpituuutta h = 0.1. Osaatko selittää syntyvän ilmiön?
172. Tutki alkuarvoprobleeman y' = x - y2, y(0) = a ratkaisuja kokeellisesti antamalla vakiolle a erilaisia arvoja ja ratkaisemalla yhtälö numeerisesti. Määritä kolmen desimaalin tarkkuudella sellainen arvo, että sen eri puolilla ratkaisut käyttäytyvät oleellisesti eri tavoin.
173. Määritä seuraavien käyräparvien kohtisuorat leikkaajat (parviparametri C; a, b, p
vakioita). Piirrä kuvio.
a) 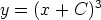
b) 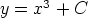
c) 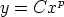
d) 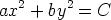
e) 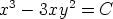
174. Määritä sellainen käyrä, joka leikkaa kohtisuorasti sekä parvea y = 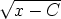 että parvea
y = e2x + C. Piirrä kuvio.
että parvea
y = e2x + C. Piirrä kuvio.
175. Käyräparvi muodostuu paraabeleista, joiden akselina on y-akseli, polttopisteenä origo ja jotka aukeavat ylöspäin. Muodosta parven differentiaaliyhtälö ja kohtisuorien leikkaajien differentiaaliyhtälö. Miten nämä suhtautuvat toisiinsa?
176. Määritä napakoordinaateissa annettujen käyräparvien
a) 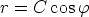
b) 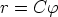
kohtisuorat leikkaajat. Piirrä kuvio.
177. Etsi käyräparvi, joka leikkaa paraabeliparven y = Cx2 kulmassa 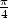 .
.
178. Käyräparven differentiaaliyhtälö napakoordinaateissa olkoon F(r,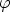 ,
,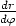 ) = 0. Mikä on
sen parven differentiaaliyhtälö napakoordinaateissa, joka leikkaa em. parven kulmassa
) = 0. Mikä on
sen parven differentiaaliyhtälö napakoordinaateissa, joka leikkaa em. parven kulmassa
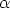 ?
?
179. Määritä ne käyrät, joilla kiinteästä muuttujan arvosta laskettu kaarenpituus on suoraan verrannollinen tangentin suuntakulman tangenttiin.
180. Etsi ne käyrät, joilla x-akselin, käyrän pisteeseen osoittavan paikkavektorin ja tähän pisteeseen asetetun tangentin muodostaman kolmion ala on vakio (= a).
181. Käyrän jokaisella normaalilla on seuraava ominaisuus: Normaalin ja käyrän leikkauspisteen etäisyys normaalin ja x-akselin leikkauspisteestä on vakio d. Millainen käyrä on kyseessä?
182. Säiliössä on m kg suolaliuosta, jonka suolapitoisuus on p0 prosenttia. Säiliöön virtaa nopeudella q1 kg/min suolaliuosta, jonka pitoisuus on p1 prosenttia, ja se sekoittuu säiliössä olevaan liuokseen siten, että liuos kaiken aikaa säilyy homogeenisena. Samaan aikaan homogeenista liuosta virtaa ulos nopeudella q2 kg/min. Muodosta säiliössä olevaa suolamäärää s(t) kuvaava alkuarvoprobleema ja ratkaise se laskentaohjelmalla. Olkoon m = 10 kg, p0 = 5 % . Piirrä suolamäärän kuvaaja tapauksissa a) p1 = 7 %, q1 = 0.6 kg/min, q2 = 0.5 kg/min, b) p1 = 3 %, q1 = q2 = 0.5 kg/min. Määritä liuoksen suolamäärä ja suolapitoisuus tunnin kuluttua.
183. Oletetaan, että kappaleen putoamista vastustaa nopeuden neliöön verrannollinen voima,
jolloin nopeus v(t) toteuttaa Newtonin lain mukaan differentiaaliyhtälön mv' = mg -av2. Tässä
t on aika, m kappaleen massa, g maan vetovoiman kiihtyvyys ja a positiivinen vakio. Ratkaise
yhtälö alkuehdolla v(0) = v0 laskentaohjelmaa käyttäen. Määritä ns. rajanopeus lim t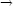
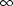 v(t).
Mikä on tämän fysikaalinen merkitys? Riippuuko rajanopeus alkunopeudesta v0? Määritä
rajanopeus, kun kyseessä on laskuvarjohyppääjä, joka painaa m = 80 kg, hänen nopeutensa
varjon auetessa on v0 = 10 m/s, maan vetovoiman kiihtyvyydelle käytetään arvoa g = 9.8 m/s2
ja hidastuvuuskerroin on a = 30 kg/m.
v(t).
Mikä on tämän fysikaalinen merkitys? Riippuuko rajanopeus alkunopeudesta v0? Määritä
rajanopeus, kun kyseessä on laskuvarjohyppääjä, joka painaa m = 80 kg, hänen nopeutensa
varjon auetessa on v0 = 10 m/s, maan vetovoiman kiihtyvyydelle käytetään arvoa g = 9.8 m/s2
ja hidastuvuuskerroin on a = 30 kg/m.
184. Nesteeseen upotettu massa m on ripustettu pystysuoraan kierrejouseen, jonka jousivakio on k. Massa saatetaan pystysuoraan värähdysliikkeeseen antamalla sille alkupoikkeama ja alkunopeus; lisäksi siihen vaikuttaa ajan mukana muuttuva pystysuora ulkoinen voima F(t). Neste vastustaa liikettä nopeuteen verrannollisella voimalla (verrannollisuuskerroin = c). Johda systeemiä kuvaava differentiaaliyhtälö.
185. Nesteeseen upotettu massa m on ripustettu pystysuoraan kierrejouseen. Massan
pystysuoraa liikettä kuvaa tällöin differentiaaliyhtälö my'' + cy' + ky = F(t), missä k on
jousivakio, kerroin c kuvaa nesteestä aiheutuvaa kitkaa ja F(t) on massaan vaikuttava ulkoinen
ajan mukana muuttuva pystysuora voima. Aseta ulkoinen voima jaksolliseksi: F(t) = F0 cos 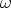 t.
Valitse yhtälössä oleviksi vakioiksi esimerkiksi m = 1, k = 5, c = 2, F0 = 1,
t.
Valitse yhtälössä oleviksi vakioiksi esimerkiksi m = 1, k = 5, c = 2, F0 = 1, 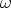 = 1. Tutki
systeemin käyttäytymistä erilaisilla alkuehdoilla ajan funktiona. Mitä mahdetaan
tarkoittaa ratkaisun transientilla komponentilla ja tasapainotilaratkaisulla (steady state
solution)?
= 1. Tutki
systeemin käyttäytymistä erilaisilla alkuehdoilla ajan funktiona. Mitä mahdetaan
tarkoittaa ratkaisun transientilla komponentilla ja tasapainotilaratkaisulla (steady state
solution)?
186. Nesteeseen upotettu massa m on ripustettu pystysuoraan kierrejouseen ja siihen
vaikuttaa ulkoinen ajan mukana muuttuva pystysuora jaksollinen voima F(t) = F0 cos 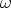 t. Jos k
on jousivakio ja kerroin c kuvaa nesteestä aiheutuvaa kitkaa, massan pystysuoraa liikettä kuvaa
differentiaaliyhtälö my'' + cy' + ky = F(t). Aseta c = 0, jolloin neste ei vastusta liikettä ja etsi
joko kokeellisesti tai laskemalla sellainen voiman F(t) taajuus
t. Jos k
on jousivakio ja kerroin c kuvaa nesteestä aiheutuvaa kitkaa, massan pystysuoraa liikettä kuvaa
differentiaaliyhtälö my'' + cy' + ky = F(t). Aseta c = 0, jolloin neste ei vastusta liikettä ja etsi
joko kokeellisesti tai laskemalla sellainen voiman F(t) taajuus 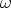 , että systeemi on resonanssissa:
heilahtelun amplitudi kasvaa rajatta (ja systeemi räjähtää rikki). Miten systeemi käyttäytyy,
kun
, että systeemi on resonanssissa:
heilahtelun amplitudi kasvaa rajatta (ja systeemi räjähtää rikki). Miten systeemi käyttäytyy,
kun 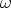 on resonanssikohdan lähellä?
on resonanssikohdan lähellä?
187. Nesteeseen upotettu massa m on ripustettu pystysuoraan kierrejouseen ja siihen
vaikuttaa ulkoinen ajan mukana muuttuva pystysuora jaksollinen voima F(t) = F0 cos 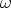 t. Jos k
on jousivakio ja kerroin c kuvaa nesteestä aiheutuvaa kitkaa, massan pystysuoraa liikettä kuvaa
differentiaaliyhtälö my'' + cy' + ky = F(t). Jos c = 0, jolloin neste ei vastusta liikettä, on
mahdollista löytää taajuus
t. Jos k
on jousivakio ja kerroin c kuvaa nesteestä aiheutuvaa kitkaa, massan pystysuoraa liikettä kuvaa
differentiaaliyhtälö my'' + cy' + ky = F(t). Jos c = 0, jolloin neste ei vastusta liikettä, on
mahdollista löytää taajuus 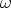 , jolla systeemi on resonanssissa, ts. heilahtelun amplitudi kasvaa
rajatta (ja systeemi räjähtää rikki). Tutki kokeellisesti, onko tämä mahdollista, jos
, jolla systeemi on resonanssissa, ts. heilahtelun amplitudi kasvaa
rajatta (ja systeemi räjähtää rikki). Tutki kokeellisesti, onko tämä mahdollista, jos
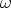
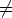 0.
0.
188. Maapallon läpi keskipisteen kautta porataan tunneli ja tähän pudotetaan kivi. Kiven liikettä kuvaa differentiaaliyhtälö mx''(t) = -kx(t), missä x(t) on kiven etäisyys maapallon keskipisteestä hetkellä t, kiven massa on m ja k on liikettä karakterisoiva positiivinen vakio. Kivi pudotetaan tunneliin antamatta sille alkunopeutta. Laske, miten pitkän ajan kuluttua kivi palaa lähtökohtaansa ja mikä on sen nopeus maapallon keskipisteen kohdalla. Maapallon säde on R = 6370 km ja maan vetovoiman kiihtyvyys x'' (0) = -g = -9.81 m/s2.
189. Heiluri, joka muodostuu painottoman varren (pituus L) päässä olevasta massasta m,
saatetaan heilahtelemaan pystysuorassa tasossa. Heilahduskulma olkoon 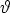 . Muodosta Newtonin
lakien mukainen liikeyhtälö, johda vastaava normaaliryhmä ja totea se autonomiseksi. Muodosta
normaaliryhmästä faasitasokäyrien differentiaaliyhtälö ja ratkaise se. Piirrä ratkaisukäyrien
kuvaajia.
. Muodosta Newtonin
lakien mukainen liikeyhtälö, johda vastaava normaaliryhmä ja totea se autonomiseksi. Muodosta
normaaliryhmästä faasitasokäyrien differentiaaliyhtälö ja ratkaise se. Piirrä ratkaisukäyrien
kuvaajia.
190. Utopian valtakunnassa väestö haluaa sitä vähemmän hyödykkeitä, mitä enemmän se on jo niitä hankkinut. Niinmuodoin elintason nousu on kääntäen verrannollinen jo saavutettuun elintasoon. Tutki, kasvaako elintaso rajatta Utopiassa. Voidaanko tällä mallilla kuvata Utopian elintasoa hamasta muinaisuudesta kaukaiseen tulevaisuuteen?