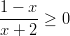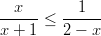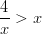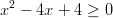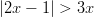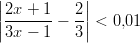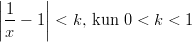Epäyhtälöt

Epäyhtälöiden ratkaiseminen perustuu usein vastaavan yhtälön ratkaisemiseen, minkä lisäksi on tarkasteltava esiintyvien lausekkeiden merkkejä.
Graafisten esitysten tekeminen, kuten sopivien funktioiden kuvaajien piirtäminen auttaa usein hahmottamaan tilannetta.

Esimerkkejä
- Ratkaistaan epäyhtälö seuraavasti:
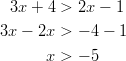

- Ratkaistaan itseisarvoepäyhtälö:
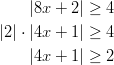

Voidaan suorittaa neliöönkorotus, koska kummatkin puolet ovat ei-negatiivisia: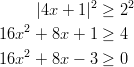
Yhtälön
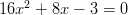 nollakohdat ovat
nollakohdat ovat 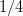 ja
ja 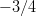 .
Paraabeli on ylöspäin aukeava, joten se on x-akselin alla nollakohtiensa
välissä.
.
Paraabeli on ylöspäin aukeava, joten se on x-akselin alla nollakohtiensa
välissä.
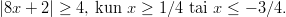
- Ratkaistaan murtoepäyhtälö
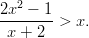
Tapa1:
Siirretään x vasemmalle puolelle ja lavennetaan nimittäjät samoiksi.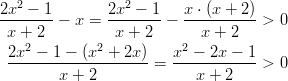

Nimittäjän pitää olla erisuurta kuin nolla, eli pitää olla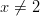 .
.
Osoittajan nollakohdat: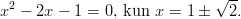
Merkkikaavio:

Taulukosta nähdään, että murtolauseke on positiivinen, kun

Tapa2:
Kerrotaan epäyhtälö :lla molemminpuolin, saadaan kaksi
2.asteen polynomia ja käsitellään kahdessa osassa:
:lla molemminpuolin, saadaan kaksi
2.asteen polynomia ja käsitellään kahdessa osassa:  ja
ja
 . (Negatiivisella luvulla puolittain kertominen kääntää
merkin!)
. (Negatiivisella luvulla puolittain kertominen kääntää
merkin!)
- Murtoepäyhtälöiden
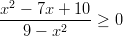 ja
ja 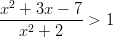 ratkaisuja.
ratkaisuja. Esimerkki 1 epäyhtälöistä
Esimerkki 1 epäyhtälöistä Esimerkki 3 epäyhtälöistä
Esimerkki 3 epäyhtälöistä
- Ratkaistaan itseisarvoepäyhtälö
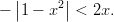
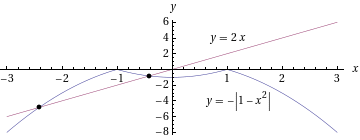
Kuvasta arvioidaan, että epäyhtälö pätee kun on noin välin
on noin välin
![[− 2,5;− 0,5]](epayhtalo20x.gif) ulkopuolella.
ulkopuolella.
Kerrotaan yhtälön molemmat puolet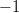 :llä, jolloin samalla merkki
kääntyy.
:llä, jolloin samalla merkki
kääntyy.


Kaksoisepäyhtälö voidaan käsitella kahdessa osassa.

Etsitään nollakohdat.
![− x2 + 2x + 1 = 0 x2 + 2x − 1 = 0 ∘ -2------------- ∘ -2------------- x = −-2-±---2--−-4-⋅ 1 ⋅-(−-1) x = −-2-±---2--−-4-⋅ 1-⋅ (− 1) √ -- − 1 ⋅ 2 √ --1 ⋅ 2 x = 1 ± 2 x = − 1 ± 2 √-- √-- 1 + 2 ⁄∈ [− 1,1] − 1 + 2 ∈ ] − 1,1[](epayhtalo25x.gif)
Kaikki nollakohdat eivät ole määrittelyväleillä ja niitä ei siksi oteta huomioon. Tehdään merkkikaaviot.

Kaaviosta nähdään:
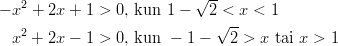
Epäyhtälö pätee pisteessä
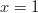 , mutta ei
, mutta ei 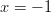 . Yhdistetään
tulokset ja saadaan vastaus:
. Yhdistetään
tulokset ja saadaan vastaus:
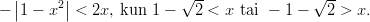
- Kolmannen asteen polynomiepäyhtälö
 .
. Esimerkki 2 epäyhtälöistä
Esimerkki 2 epäyhtälöistä
- Ratkaistaan itseisarvoepäyhtälö
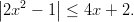

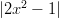 :n nollakohdat ovat
:n nollakohdat ovat 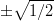 ja epäyhtälö voidaan jakaa
kahteen tarkasteltavaan osaan:
ja epäyhtälö voidaan jakaa
kahteen tarkasteltavaan osaan:
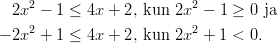
Aloitetaan ensimmäisestä, joka saadaan muotoon
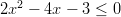 .
Nollakohdiksi tulevat
.
Nollakohdiksi tulevat 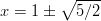 . Merkkikaavioon merkitään
epäyhtälön ja sen ehdon,
. Merkkikaavioon merkitään
epäyhtälön ja sen ehdon, 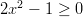 , merkit eri nollakohtien
väleissä. Kaaviosta voidaan tarkastella kumpaakin polynomia erikseen ja
rajaamaan kummankin toivotut välit.
, merkit eri nollakohtien
väleissä. Kaaviosta voidaan tarkastella kumpaakin polynomia erikseen ja
rajaamaan kummankin toivotut välit.

Epäyhtälö pätee, kun
 , mutta
, mutta 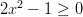 , eli
taulukon mukaan välillä
, eli
taulukon mukaan välillä 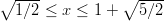 .
.
Jälkimmäisen, , nollakohdiksi tulevat
, nollakohdiksi tulevat
 .
.

Vastaavasti
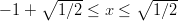 . Lopuksi tulokset yhdistetään ja
saadaan vastaukseksi väli
. Lopuksi tulokset yhdistetään ja
saadaan vastaukseksi väli
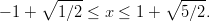
- Trigonometrinen epäyhtälö
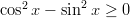 .
. Esimerkki 4 epäyhtälöistä
Esimerkki 4 epäyhtälöistä
- Epäyhtälön
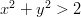 tulkinta.
tulkinta. Esimerkki 5 epäyhtälöistä
Esimerkki 5 epäyhtälöistä

Harjoitustehtäviä
- Ratkaise epäyhtälöt:
-
- Ratkaise toisen asteen epäyhtälöt:
-
- Ratkaise itseisarvoepäyhtälöt:
-
Tehtävien vastaukset: