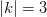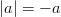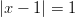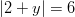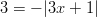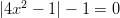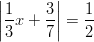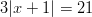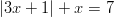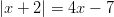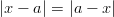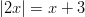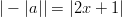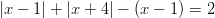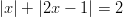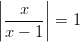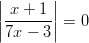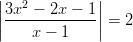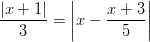Itseisarvoyhtälöt

Itseisarvolausekkeisiin ja itseisarvoyhtälöihin tai itseisarvoepäyhtälöihin johdutaan usein määritettäessä lukujen etäisyyksiä ja tason tai avaruuden pisteiden välisiä etäisyyksiä. Usein on myös tarpeen johtaa yläraja-arvioita itseisarvolausekkeille esimerkiksi numeerisen laskennan virhetermejä arvioitaessa.
Itseisarvolausekkeien muokkaaminen ja tarvittaessa niitä sisältävien yhtälöiden tai epäyhtälöiden ratkaiseminen onkin matematiikassa usein käytetty työkalu.

Esimerkkejä
- Ratkaistaan itseisarvoyhtälö:
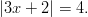
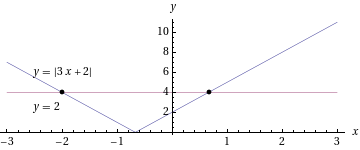
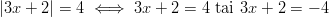
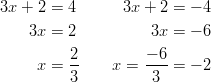
Yhtälö pätee, kun
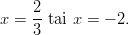
- Ratkaistaan

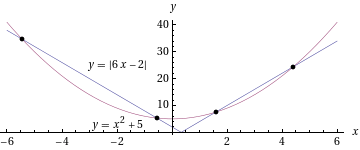
Yhtälössä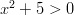 , jolloin voimme todeta, että
, jolloin voimme todeta, että 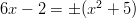 :
:
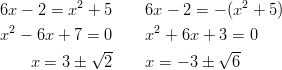
Itseisarvoyhtälö pätee, kun
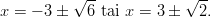
- Ratkaistaan

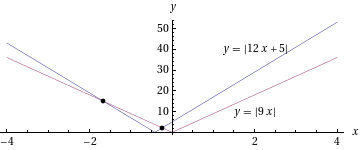
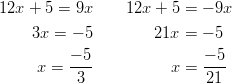
Yhtälön ratkaisut ovat
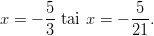

Harjoitustehtäviä
- Ratkaise:
-
- Ratkaise:
-
- Ratkaise:
-
- Ratkaise:
-
- Ratkaise:
-
- Ratkaise:
-
Tehtävien vastaukset: