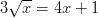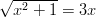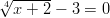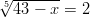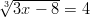Juuriyhtälöt

Käsiteltäessä parillisindeksisiä juuria reaalialueella oletetaan yleensä, että juurimerkintä tarkoittaa positiivista vaihtoehtoa. Juuren merkkiin onkin kiinnitettävä erityistä huomiota. Hyvä esimerkki on juuriyhtälön ratkaiseminen. Juuret voidaan usein poistaa korottamalla yhtälön molemmat puolet neliöön tai johonkin muuhun potenssiin. Tällöin saatava yhtälö ei välttämättä ole yhtäpitävä alkuperäisen kanssa, vaan sillä voi olla muitakin juuria. Saattaa myös olla, että neliöön korotetulla yhtälöllä on juuria, vaikka alkuperäisellä ei ole lainkaan ratkaisua.
Usein tilanteen tutkimisessa helpoin tapa on piirtää sopivat funktioiden kuvaajat, joiden avulla voi hahmottaa tilanteen.

Esimerkkejä
- Ratkaistaan juuriyhtälö
 .
.
Yhtälöllä ei ole yhtään reaalista ratkaisua, koska neliöjuuri on aina ei-negatiivinen eikä koskaan .
. 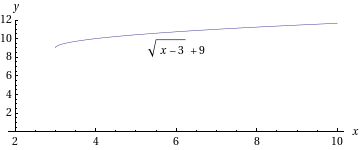
- Ratkaistaan juuriyhtälö
 .
.
Neliöjuuri on määritelty, kun , eli kun
, eli kun 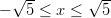 .
Järjestellään termejä ja suoritetaan neliöönkorotus, joka rajaa
määrittelyjoukkoa ehdolla
.
Järjestellään termejä ja suoritetaan neliöönkorotus, joka rajaa
määrittelyjoukkoa ehdolla 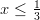 .
.
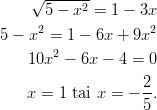
Toisen asteen yhtälön ratkaisuista vain
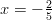 sopii määrittelyvälille
ja on juuriyhtälön ainoa ratkaisu.
sopii määrittelyvälille
ja on juuriyhtälön ainoa ratkaisu. 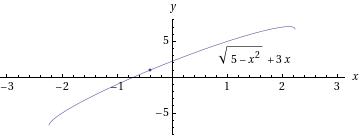
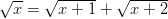
 Esimerkki juuriyhtälön ratkaisusta
Esimerkki juuriyhtälön ratkaisusta
- Ratkaistaan juuriyhtälö
 .
.
Yhtälön neliöjuuren takia: .
.
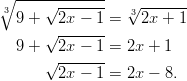
Jotta yhtälö pätisi, pitää olla
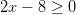 eli
eli 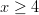 . Suoritetaan
neliöönkorotus:
. Suoritetaan
neliöönkorotus:
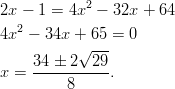
Vain ratkaisu
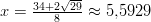 täyttää ehdon
täyttää ehdon 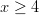 ja
toteuttaa alkuperäisen yhtälön eli se on ainut ratkaisu.
ja
toteuttaa alkuperäisen yhtälön eli se on ainut ratkaisu. 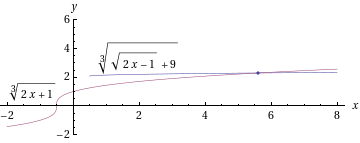

Harjoitustehtäviä
- Ratkaise neliöjuuriyhtälön reaaliset juuret:
-
- Ratkaise yhtälö:
-
- Ratkaise juuriyhtälöt:
-
Tehtävien vastaukset: