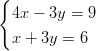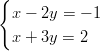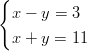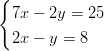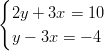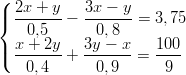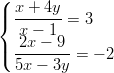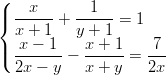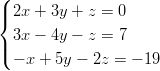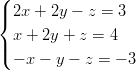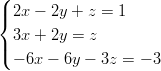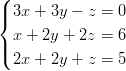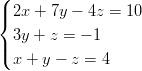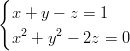Yhtälöryhmät

Yhtälöryhmien ratkaisemisessa yleispätevä menettely on ratkaista jostakin yhtälöstä yksi tuntematon muiden avulla ja sijoittaa saatu lauseke muihin yhtälöihin. Tällä tavoin ryhmä redusoidaan pienemmäksi: tuntemattomia on yksi vähemmän, samoin yhtälöitä.
Lineaarisen yhtälöryhmän — tuntemattomat esiintyvät vain ensimmäisessä potenssissa eikä niiden tuloja esiinny — menettely on helppo toteuttaa systemaattisesti; siitä käytetään nimtystä Gaussin algoritmi. Jos yhtälöryhmä on epälineaarinen — muunlainen — ei em. periaatetta välttämättä voi toteuttaa lainkaan ja ainoaksi mahdollisuudeksi jää yhtälöryhmän ratkaiseminen numeerisesti. Numeerisia menettelyjä on monia erilaisia ja sopivin riippuu yhtälöryhmän erityisominaisuuksista.

Esimerkkejä
- Ratkaistaan lineaarinen yhtälöpari
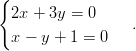
Tapa 1:
Kerrotaan alempi yhtälö kolmella ja lasketaan yhtälöt puolittain yhteen:

Tehdään sijoitus:
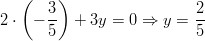
Lopuksi kannattaa tarkistaa tulos. Yhtälöryhmä pätee, kun
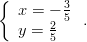
Tapa 2:
Ratkaistaan alempi yhtälö :n suhteen ja sijoitetaan ylempään
lausekkeeseen.
:n suhteen ja sijoitetaan ylempään
lausekkeeseen.
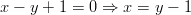

Nyt voidaan ratkaista
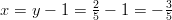 ja saatu vastaus on sama
kuin 1. tavalla.
ja saatu vastaus on sama
kuin 1. tavalla.
- Kaksi lineaarista yhtälöryhmää.
 Esimerkki 1 yhtälöryhmän ratkaisemisesta
Esimerkki 1 yhtälöryhmän ratkaisemisesta Esimerkki 2 yhtälöryhmän ratkaisemisesta
Esimerkki 2 yhtälöryhmän ratkaisemisesta
- Ratkaistaan yhtälöpari
 .
.
Lasketaan yhtälöt auki ja vähennetään alempi ylemmästä rivistä ja ratkaistaan toinen muuttuja:
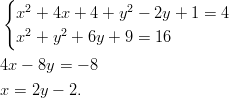
Sijoitetaan saatu ratkaisu toiseen yhtälöistä.
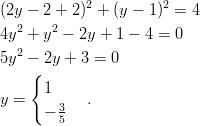
Sijoitetaan ratkaisut yhtälöön
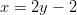 .
.
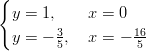
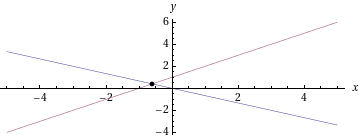
Ratkaisut ovat pisteet
 ja
ja  .
. 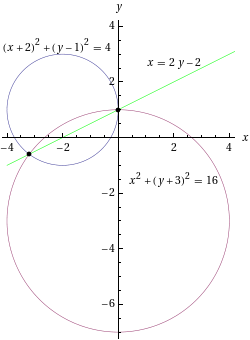
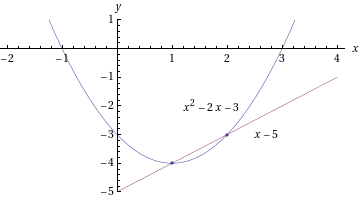
- Epälineaarinen yhtälöpari:
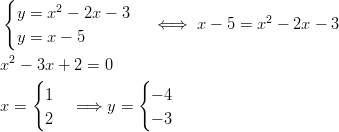
Ratkaisut ovat
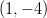 ja
ja 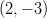 .
. 

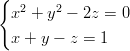

Harjoitustehtäviä
- Ratkaise lineaariset yhtälöparit:
-
- Ratkaise:
-
- Ratkaise:
-
- Ratkaise epälineaariset yhtälöryhmät:
-
Tehtävien vastaukset: