Jaollisuus ja alkuluvut

Kokonaislukujen joukko on = {0,±1,±2,...}.

Jos kokonaisluku a on jaollinen kokonaisluvulla b, toisin sanoen on olemassa sellainen kokonaisluku c, että a = bc, merkitään b | a. Tällöin sanotaan, että b jakaa luvun a, b on luvun a tekijä tai a on luvun b monikerta. Jos a ei ole luvun b monikerta merkitään b a.

Esimerkki. 2 | 10, (-3) | 9, 5 11.

Jaollisuudella on seuraavat yksinkertaiset ominaisuudet:

     (a)   1 | a a
     (b)   a | a a
     (c)   jos a | b ja b | a, niin a = ±b
     (d)   jos a | b ja b | c, niin a | c
     (e)   jos a | b ja a | c, niin a | (ub + vc) kaikilla u,v

Todistetaan kohta (e) ja jätetään muiden kohtien miettiminen harjoitukseksi. Oletetaan, että a | b ja a | c, silloin on olemassa sellaiset luvut r ja s, että ub + vc = u(ar) + v(as) = a(ur + vs), joten a | (ub + vc).

Määritelmä. Kokonaislukua p > 1, jonka ainoat tekijät ovat ±1 ja ±p, sanotaan alkuluvuksi. Muita kokonaislukuja sanotaan yhdistetyiksi luvuiksi.

Alkulukujen joukosta käytetään merkintää 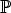, siis

Lause. Alkulukuja on äärettömän monta.

Todistus. Tehdään vastaoletus, että p₁,...,p_k ovat kaikki alkuluvut. Muodostetaan luku n = p₁ p₂ p_k + 1. Koska alkulukuja ylipäänsä on olemassa, on n > 1 ja täten se voidaan hajottaa tekijöihin. On siis olemassa sellainen alkuluku q, että q | n. Koska p₁ , ... , p_k ovat kaikki alkuluvut, niin voidaan olettaa, että q = p_i. On olemassa sellainen kokonaisluku c, että p₁p_k + 1 = cp_i, siis 1 = p_i(c - p₁p_i-1p_i+1p_k). Koska c - p₁ p_i-1 p_i+1p_k niin p_i | 1, mikä on mahdotonta, sillä p_i on alkuluku.

Linkit:
Jakoalgoritmi