Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003 		LINEAARIALGEBRA
 

Esimerkkejä vektoriavaruuksista

Esimerkki. Määritellään joukossa

Rn = {(x1, ...,xn)| x1 (- R,...,xn (- R}

summa ja skalaaritulo seuraavasti:

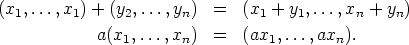
(x1,...,x1) + (y2,...,yn) = (x1 + y1,...,xn + yn) a(x ,...,x ) = (ax ,...,ax ). 1 n 1 n
Tarkistamalla vektoriavaruuden kaikkien postulaattien V1-V8 toteutuvuus huomataan, että kolmikko (Rn, +, . ) on vektoriavaruus. Tämän vektoriavaruuden nollavektori on h = 0 = (0,..., 0) ja vektorin (x1,...,xn) vastavektori on (-x1,...,-xn).

Esimerkki. Kaikkien reaalifunktioiden joukko on

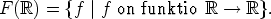
F (R) = {f |f on funktio R --> R}.

Kuten kaikissa funktiojoukoissa on tässäkin funktioiden yhtäsuuruus ymmärrettävä seuraavasti:

f = g <==> f(x) = g(x) A x (tässäsiis A x (- R).

Kolmikko (F (R), +, . ) on vektoriavaruus, kun määritellään

f + g : (f + g)(x) = f(x) + g(x) A x (- R, af : (af )(x) = a .f(x) A a, x (- R.

Tällöin f + g (- F(R) ja af (- F(R). Kolmikko todetaan vektoriavaruudeksi käymällä läpi vektoriavaruuden postulaatit. Esimerkiksi postulaatti V1 seuraa siitä, että f(x) + g(x) = g(x) + f(x) kaikilla reaaliluvuilla x. Vektoriavaruuden nolla-alkio on f0 (x) = 0 A x (- R, sillä kaikilla f (- F(R) on (f + f0)(x) = f(x) + f0(x) = f(x) + 0 = f(x). Vektoriavaruuden funktion f vasta-alkio on -f : (-f)(x) = -f(x) kaikilla x (- R. Nimittäin kaikilla f (- F (R) on (f + (-f))(x) = f(x) + (-f(x)) = 0.

Linkit:
Vektoriavaruus