| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | LINEAARIALGEBRA |
Vektoriavaruus
Määritelmä. Kolmikko (V, +, . ) on vektoriavaruus, jos V on epätyhjä joukko, jossa on
määritelty alkioiden summa X + Y (+ on funktio V ×V  V ) ja skalaarimonikerta aX ( . on
funktio
V ) ja skalaarimonikerta aX ( . on
funktio  × V
× V  V, . jätetään usein merkitsemättä) ja lisäksi nämä operaatiot toteuttavat
seuraavat ehdot:
V, . jätetään usein merkitsemättä) ja lisäksi nämä operaatiot toteuttavat
seuraavat ehdot:
V1. X + Y = Y + X kaikilla X,Y  V (kommutatiivisuus eli vaihdantalaki),
V (kommutatiivisuus eli vaihdantalaki),
V2. (X + Y ) + Z = X + (Y + Z) kaikilla X,Y,Z  V (assosiatiivisuus eli liitäntälaki),
V (assosiatiivisuus eli liitäntälaki),
V3. on olemassa sellainen 
 V , että X +
V , että X +  = X kaikilla X
= X kaikilla X  V (nolla-alkio),
V (nolla-alkio),
V4. kaikilla X  V on olemassa sellainen -X
V on olemassa sellainen -X  V, että X + (-X) =
V, että X + (-X) =  (vasta-alkio),
(vasta-alkio),
V5. a(X + Y ) = aX + aY kaikilla a 
 ja X,Y
ja X,Y  V,
V,
V6. (a + b)X = aX + bX kaikilla a,b 
 ja X
ja X  V,
V,
V7. a(bX) = (ab)X kaikilla a,b 
 ja X
ja X  V,
V,
V8. 1X = X kaikilla X  V (tässä luku 1 on reaaliluku yksi).
V (tässä luku 1 on reaaliluku yksi).
Vektoriavaruuden alkioita kutsutaan vektoreiksi. Samoin puhutaan myös nollavektorista  ja
alkion X vastavektorista -X.
ja
alkion X vastavektorista -X.
Vektoriavaruudesta (V, +, . ) voidaan lyhyesti puhua vain vektoriavaruutena V, jos vektoriavaruuden operaatiot ovat selviä asiayhteydestä.
Lause. Vektoriavaruuden nollavektori ja alkion X vastavektori -X ovat yksikäsitteisiä.
Todistus. Tehdään vastaoletus, että vektoriavaruudella (V, +, . ) on kaksi nollavektoria  ja
ja  '.
Tarkastellaan nollavektoreiden summaa
'.
Tarkastellaan nollavektoreiden summaa  +
+  '. Postulaatin V3 mukaan nollavektorin lisääminen
ei muuta vektoria, joten
'. Postulaatin V3 mukaan nollavektorin lisääminen
ei muuta vektoria, joten  +
+  ' =
' =  . Samasta syystä
. Samasta syystä  ' +
' +  =
=  '. Toisaalta ensimmäisen
postulaatin mukaan
'. Toisaalta ensimmäisen
postulaatin mukaan  +
+  ' =
' =  ' +
' +  , joten
, joten  =
=  '.
'.
Oletaan, että vektorilla X on vastavektorit -X ja X'. Lisäämällä yhtälön X + X' =  molemmille puolille -X saadaan vasemmasta puolesta käyttämällä postulaatteja V2, V4, V1 ja
V3,
molemmille puolille -X saadaan vasemmasta puolesta käyttämällä postulaatteja V2, V4, V1 ja
V3,
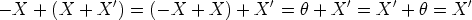
ja oikeasta puolesta postulaatin V3 nojalla -X +  = -X. Täten X' = -X.
= -X. Täten X' = -X. ![[]](images/msam10-c-3.gif)
Linkit:
Esimerkkejä vektoriavaruuksista
Vektoriavaruuden ominaisuuksia