| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | LINEAARIALGEBRA |
Vektoriavaruuden ominaisuuksia
Määritellään vektorien X ja Y erotus:
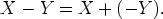
Vektoriyhtälöstä X + Y = Z voidaan ratkaista X lisäämällä vektorin Y vastavektori -Y molemmille puolille, siis
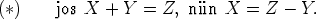
Oletetaan jatkossa, että kolmikko (V, +, . ) on vektoriavaruus.
Lause. Oletetaan, että a 
 ja X
ja X  V. Jos a = 0 tai X =
V. Jos a = 0 tai X =  , niin aX =
, niin aX =  .
.
Todistus. Oletetaan ensin, että a = 0. Koska 0X + 0X = (0 + 0)X = 0X niin päättelyn (*)
perusteella 0X = 0X - 0X =  . Jos X =
. Jos X =  , saadaan samoin a
, saadaan samoin a + a
+ a = a(
= a( +
+  ) = a
) = a ja
käyttämällä päättelyä (*) nähdään, että a
ja
käyttämällä päättelyä (*) nähdään, että a =
=  .
. ![[]](images/msam10-c-3.gif)
Lause. Olkoot a 
 ja X
ja X  V. Jos a
V. Jos a 0 ja aX =
0 ja aX =  , niin X =
, niin X =  .
.
Todistus. Oletetaan, että aX =  ja a
ja a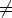 0. Silloin
0. Silloin

missä viimeinen yhtäsuuruus seuraa edellisestä lauseesta. ![[]](images/msam10-c-3.gif)
Lause. Jos X  V niin (-1) . X on alkion X vasta-alkio.
V niin (-1) . X on alkion X vasta-alkio.
Todistus. Pitää osoittaa, että X + (-1) . X =  . Saadaan
. Saadaan
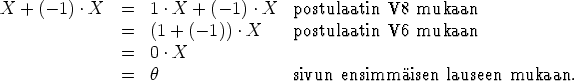
![[]](images/msam10-c-3.gif)
Edellisten lauseiden avulla saadaan kaavat -(X -Y ) = Y -X ja a(X -Y ) = aX -aY kaikilla
X, Y  V ja a
V ja a 
 . Liitäntälain V2 perusteella kolmen vektorin X,Y,Z
. Liitäntälain V2 perusteella kolmen vektorin X,Y,Z  V summa voidaan
kirjoittaa muodossa X + Y + Z. Sama pätee yleisestikin useamman vektorin summaan. Yleisesti
vektoriavaruudessa voidaan muodostaa lauseke
V summa voidaan
kirjoittaa muodossa X + Y + Z. Sama pätee yleisestikin useamman vektorin summaan. Yleisesti
vektoriavaruudessa voidaan muodostaa lauseke
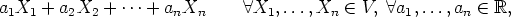
joka siis merkitsee erästä (yksikäsitteistä) vektoria. Tätä sanotaan vektorien X1,...,Xn lineaarikombinaatioksi.
Linkit:
Vektoriavaruus