Lineaarinen riippuvuus

Olkoon (V, +, ^. ) vektoriavaruus ja sen nolla-alkio. Olkoot lisäksi X ₁,...,X_m joukon V m vektoria. Jos joillakin c₁,...,c_m on

sanotaan, että vektorit X₁,...,X_m toteuttavat lineaarisen relaation. Jokainen vektorijoukko toteuttaa triviaalin lineaarisen relaation, nimittäin sen, jossa c₁ = c₂ = ... = c_m = 0. Muita lineaarisia relaatioita sanotaan epätriviaaleiksi.

Määritelmä. Jos vektorit X₁,...,X_m toteuttavat ainakin yhden epätriviaalin relaation, sanotaan, että nämä vektorit ovat lineaarisesti riippuvia. Muussa tapauksessa näitä vektoreita sanotaan lineaarisesti riippumattomiksi.

Jos vektorit X₁,...,X_m ovat lineaarisesti riippuvia (tai riippumattomia), sanotaan myös, että joukko {X₁,...,X_m} on lineaarisesti riippuva (tai riippumaton).

Yhden vektorin joukko {X} on lineaarisesti riippuva, jos aX = jollakin nollasta eroavalla reaaliluvulla a. Vektoriavaruuden ominaisuuksia -sivun toisen lauseen mukaan on tällöin vektori X = . Siis {} on lineaarisesti riippuva ja kaikille X joukko {X} on lineaarisesti riippumaton.

Lause. Vektoriavaruuden (V, +, ^. ) joukon V vähintään kahden vektorin äärellinen osajoukko on lineaarisesti riippuva jos ja vain jos jokin joukon vektori on joukon muiden vektorien lineaarikombinaatio.

Todistus. Oletetaan ensin, että joukko {X₁,...,X_m} V on lineaarisesti riippuva. Silloin on olemassa sellaiset kertoimet c₁,...,c_m, joista ainakin yksi on nollasta eroava, että

Voidaan olettaa, että c_i0. Silloin saadaan

joten X_i voidaan esittää muiden vektorien lineaarikombinaationa.

Oletetaan kääntäen, että X_i = b₁X₁ + 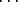+ b_i-1X_i-1 + b_i+1X_i+1 + + b_mX_m, joillekin luvuille b₁ , ... , b_i-1,b_i+1,...,b_m . Silloin

Koska vektorin X_i kerroin on nollasta eroava, vektorit X₁,...,X_m toteuttavat epätriviaalin lineaarisen relaation ja ovat siis lineaarisesti riippuvia.

Edellä todistetusta lauseesta seuraa, että kahden vektorin joukko {X₁,X₂} on lineaarisesti riippuva, jos ja vain jos toinen vektoreista on toisen skalaarimonikerta. Vektoriavaruudessa ² tämä tarkoittaa sitä, että kaksi vektoria u = (u₁,u₂) ja v = (v₁,v₂) ovat lineaarisesti riippuvia jos ja vain jos ne ovat samalla origon kautta kulkevalla suoralla.

Linkit:
Vektoriavaruuden ominaisuuksia (lineaarikombinaation määritelmä)