Vektoriavaruuden dimensio

Lause. Olkoon (V, +, ^. ) vektoriavaruus ja B = {X ₁,...,X_n} sen kanta. Silloin mikä tahansa joukon V osajoukko, jossa on m vektoria ja m > n, on lineaarisesti riippuva.

Todistus. Olkoon Y = {Y ₁,...,Y _m} V. Koska B on kanta, saadaan vektoreille Y _j (1 < j < m) kantaesitykset:

Osoitetaan, että yhtälöllä c₁Y ₁ + c₂Y ₂ + + c_mY _m = on epätriviaali ratkaisu. Sijoittamalla vektorien Y _j paikalle niiden kantaesitykset saadaan yhtälö:

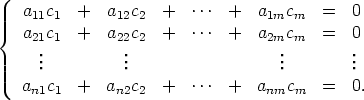
Sivulla Lineaarinen riippuvuus ja homogeeniset yhtälöryhmät todistetaan determinanttien teorian avulla, että tällä yhtälöryhmällä on epätriviaali ratkaisu (c₁,c₂,...,c_m), koska m > n. (Huomaa, että sivun Lineaarinen riippuvuus ja homogeeniset yhtälöryhmät lause, jota tässä tarvitaan, ei riipu tästä lauseesta.) Täten joukko Y on lineaarisesti riippuva.

Lause. Vektoriavaruuden kaikissa kannoissa on yhtä monta vektoria.

Todistus. Oletetaan, että jossain vektoriavaruuden kannassa B₁ olisi enemmän vektoreita kuin sen toisessa kannassa B₂. Edellisen lauseen mukaan silloin joukon B₁ vektorit ovat lineaarisesti riippuvia, mikä on vastoin kannan määritelmää.

Määritelmä. Vektoriavaruuden (V, +, ^. ) kannan B = {X ₁,...,X_n} alkioiden lukumäärää n sanotaan vektoriavaruuden dimensioksi. Dimensio on siis kannan valinnasta riippumaton. Merkitään

Sanotaan myös, että vektoriavaruus (V, +, ^. ) on n-ulotteinen.

Sivun Vektoriavaruuden kannasta lauseen mukaan jokaisella äärellisesti generoidulla vektoriavaruudella on kanta, täten myös yksikäsitteinen dimensio kuten edellinen lause osoittaa. Äärellisesti generoitua vektoriavaruutta voidaan sanoa myös äärellisulotteiseksi. Jos vektoriavaruus ei ole äärellisulotteinen, sen dimensio on ääretön.

Huomaa vielä, että tämän sivun ensimmäisen lauseen ja määritelmän mukaan vektoriavaruuden dimensio on sen suurimman mahdollisen lineaarisesti riippumattoman vektorijoukon vektorien lukumäärä.

Linkit:
Lineaarinen riippuvuus ja homogeeniset yhtälöryhmät
Vektoriavaruuden kannasta