smr050.html

Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003

LINEAARIALGEBRA

Matriisi

Määritelmä. Olkoot n,m > 1 kokonaislukuja. Jos a_ij kaikilla 1 < i < m ja 1 < j < n, niin taulukkoa

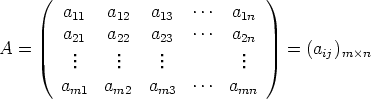
( ) a11 a12 a13 ... a1n a21 a22 a23 ... a2n A = .. .. .. .. = (aij)m×n . . . . am1 am2 am3 ... amn

sanotaan (m × n)-matriisiksi. Merkinnässä (a_ij) luku i tarkoittaa siis vaakariviä ja luku j pystyriviä.

Käytetään merkintää (i,j) matriisin i :nnen vaakarivin ja j :nnen pystyrivin leikkauksessa olevasta paikasta.

Matriisin alkiot voivat olla myös kompleksilukuja tai yleisemmin tietyt ehdot täyttävän joukon alkioita. Käsitellään nyt kuitenkin vain reaalilukualkioisia matriiseja.

Kaksi matriisia A = (a_ij)_m×n ja B = (b_ij)_h×k ovat samaa tyyppiä, jos m = h ja n = k. Jos lisäksi a_ij = b_ij kaikilla lukujen i ja j arvoilla ovat matriisit A ja B yhtäsuuret.

Jos matriisin A vaakarivit vaihdetaan pystyriveiksi saadaan matriisin A transponoitu matriisi A^T, siis

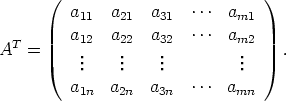
( ) a11 a21 a31 ... am1 a a a ... a AT = 12. 22. 32. m.2 . .. .. .. .. a1n a2n a3n ... amn

Transponoitu matriisi on tyyppiä n × m. Vektorin X = (x₁,...,x_n) voidaan ajatella olevan (1 × n)-matriisi. Silloin siis

( ) x1 XT = ... . xn

Vektoria X voidaan sanoa vaakavektoriksi ja matriisia X^T pystyvektoriksi.

Matriisin A i :nnestä vaakarivistä voidaan käyttää lyhennysmerkintää A_i. Vastaavasti j :nnestä pystyrivistä eli sarakkeesta voidaan käyttää merkintää A^(j). Siis

( A ) .1 (1) (n) A = (aij)m× n = .. = (A ,...,A ), Am

missä

Ai = (ai1,ai2,...,ain) (i = 1,...,m) A(j) = (a1j,a2j,...,amj)T (j = 1,...,n).

Linkit:
Yksinkertaisia matriiseja