Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003 		LINEAARIALGEBRA
 

Yksinkertaisia matriiseja

Yksittäisen reaaliluvun a voidaan ajatella tarkoittavan (1 × 1)-matriisia (a).

Jos matriisissa A = (aij)m×n on n = m, puhutaan neliömatriisista.

Nollamatriisi on (m × n)-matriisi, jonka kaikki alkiot ovat nollia, siis

( ) 0 0 ... 0 0 0 ... 0 0 = .. .. .. . . . . 0 0 ... 0

Matriisin A sanotaan olevan symmetrinen, jos AT = A. Symmetrisen matriisin on välttämättä oltava neliömatriisi.

Olkoon A = (aij)n×n neliömatriisi. Alkiot a11,a22,...,ann muodostavat matriisin (pää)lävistäjän eli diagonaalin. Jos aij = 0 kaikilla i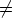/=j, sanotaan, että matriisi A on lävistäjä- eli diagonaalimatriisi:

( ) a11 0 ... 0 0 a22 ... 0 .. .. .. . . . . 0 0 ... ann

Selvästi jokainen diagonaalimatriisi on symmetrinen matriisi.

Identiteettimatriisiksi In sanotaan (n × n)-diagonaalimatriisia, jonka kaikki diagonaalialkiot ovat ykkösiä. Siis

( ) 1 0 ... 0 0 1 ... 0 In = .. .. .. . . . . 0 0 ... 1

Linkit:
Matriisi