smr054.html

Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003

LINEAARIALGEBRA

Matriisitulon ominaisuuksia

Lause. (Assosiatiivilaki) Olkoot A = (a_ij)_n×m, B = (b_ij)_m×p ja C = (c_ij)_p×q matriiseja. Silloin

A(BC) = (AB)C.

Todistus. Matriisin AB paikassa (i,j) (1 < i < n, 1 < j < p) on alkio sum m
k=1 a_ikb_kj. Täten matriisin (AB)C paikassa (i,l) (1 < i < n, 1 < l < q) on alkio

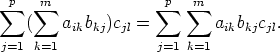
p m p m sum sum sum sum ( aikbkj)cjl = aikbkjcjl. j=1 k=1 j=1 k=1

Toisaalta matriisin BC paikassa (k,l) (1 < k < m, 1 < l < q) on alkio sum
p
j=1 b_kjc_jl ja täten matriisin A(BC) paikassa (i,l) (1 < i < n, 1 < l < q) on alkio

sum m sum p m sum sum p aik( bkjcjl) = aikbkjcjl. j=1 j=1 k=1 k=1

Koska summauksen järjestyksen vaihto ei muuta summaa, saadaan väite.

Lause. (Distributiivilait)

A(B + C) = AB + AC, (A + B)C = AC + BC.

Todistus. Todistetaan ensimmäinen distributiivilaki, toinen voidaan todistaa samoin. Merkitään A = (a_ij)_n×m, B = (b_ij)_m×p ja C = (c_ij)_m×p. Silloin B + C = (b_kj + c_kj)_m×p. Täten matriisin A(B + C) paikassa (i,j) (1 < i < n, 1 < j < p) on alkio

sum m aik(bkj + ckj). k=1

Toisaalta AB = 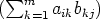sum m
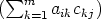( k=1aikbkj) _n×p ja AC = sum m
( k=1aikckj) _n×p, joten matriisin AB + AC paikassa (i, j) (1 < i < n, 1 < j < p) on alkio

m m sum sum aikbkj + aikckj. k=1 k=1

Koska sum
mk=1 a_ik(b_kj + c_kj) = a_ikb_kj + a_ikc_kj, saadaan väite.

Linkit:
Matriisien algebraa
Matriisitulo