| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | LINEAARIALGEBRA |
Determinantti
Määritelmä. Olkoon A (2 × 2)-matriisi ja olkoon B (3 × 3)-matriisi:

Matriisin A determinantti on
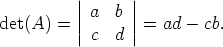
Matriisin B determinantti on

Determinantti voidaan määritellä kaikille neliömatriiseille. Yleistä määrittelyä varten esitetään ensin permutaation käsite ja joitakin siihen liittyviä käsitteitä.
Määritelmä. Jonoa (j1,j2,...,jn) sanotaan lukujen 1, 2,...,n permutaatioksi, jos jonossa ovat kaikki luvut 1, 2,...,n jossain järjestyksessä.
Permutaatiossa (j1,j2,...,jn) sanotaan paria jh,jk käännetyksi, jos h < k ja jh > jk. Käännettyä paria voidaan sanoa myös inversioksi.
Permutaatiota sanotaan parilliseksi tai parittomaksi sen mukaan, onko permutaatiossa parillinen vai pariton määrä käännettyjä pareja. Permutaation merkki on
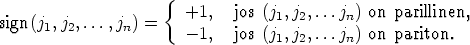
Nyt voidaan määritellä yleisen (n × n)-matriisin A = (aij) determinantti.
Määritelmä.
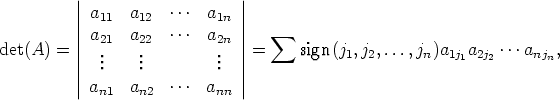
missä summaan otetaan kaikki lukujen 1, 2,...,n permutaatiot (j1,j2,...,jn).
Lukujen 1, 2, ...,n permutaatioita on n! = 1 . 2 . 3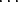 n kappaletta. Täten determinantin
yleisessä määrittelyssä yhteenlaskettavia on n! kappaletta. Luku n! kasvaa nopeasti luvun n
kasvaessa ja siksi määritelmän menetelmä determinantin laskemiseksi suurelle neliömatriisille on
tehotonta. Determinantin laskemista voidaan kuitenkin helpottaa kuten käy ilmi sivulta
Determinantin perusominaisuuksia.
n kappaletta. Täten determinantin
yleisessä määrittelyssä yhteenlaskettavia on n! kappaletta. Luku n! kasvaa nopeasti luvun n
kasvaessa ja siksi määritelmän menetelmä determinantin laskemiseksi suurelle neliömatriisille on
tehotonta. Determinantin laskemista voidaan kuitenkin helpottaa kuten käy ilmi sivulta
Determinantin perusominaisuuksia.