| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | LINEAARIALGEBRA |
Transponoidun matriisin determinantti
Lause. Olkoon A = (aij)n×n neliömatriisi. Silloin

Todistus. Olkoon A = (aij) ja merkitään AT = (b ij), missä bij = aji. Determinantin määritelmän mukaan on

Summassa ovat mukana tarkalleen kaikki sellaiset tulot, joissa on yksi alkio matriisin (bij) jokaiselta vaakariviltä ja yksi jokaiselta pystyriviltä. Siis summassa ovat mukana tarkalleen kaikki samat tulot kuin matriisin (aij) determinantin määritelmän mukaisessa summalausekkeessa. Edellä tulon tekijät on järjestetty pystyrivien mukaiseen järjestykseen; järjestämällä tulon tekijät vaakarivien mukaiseen järjestykseen saadaan
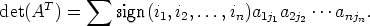
Tarkastellaan summan termiä ai11ai22 ainn = a1j1a2j2
ainn = a1j1a2j2 anjn. Nyt sign(j1,j2,...,jn) termille
a1j1a2j2
anjn. Nyt sign(j1,j2,...,jn) termille
a1j1a2j2 anjn voidaan laskea seuraavasti: Merkitään (n × n)-taulukkoon merkki X jokaiseen
kohtaan (k,jk), missä k käy läpi vaakarivit (1 < k < n). Jokaiselle riville ja sarakkeelle tulee siis
tarkalleen yksi merkki X. Kirjoitetaan jokaisella rivillä merkki O niihin merkin X
vasemmanpuoleisiin ruutuihin, joiden yläpuolella samalla sarakkeella ei ole merkkiä X.
Kaikkien merkkien O lukumäärä on käännettyjen parien lukumäärä permutaatiossa
(j1,j2,...,jn).
anjn voidaan laskea seuraavasti: Merkitään (n × n)-taulukkoon merkki X jokaiseen
kohtaan (k,jk), missä k käy läpi vaakarivit (1 < k < n). Jokaiselle riville ja sarakkeelle tulee siis
tarkalleen yksi merkki X. Kirjoitetaan jokaisella rivillä merkki O niihin merkin X
vasemmanpuoleisiin ruutuihin, joiden yläpuolella samalla sarakkeella ei ole merkkiä X.
Kaikkien merkkien O lukumäärä on käännettyjen parien lukumäärä permutaatiossa
(j1,j2,...,jn).
Termiä ai1 1 ai2 2 ainn tarkasteltaessa tehdään taas (n × n)-taulukko, jossa merkitään X :llä
ruutuja (ik , k), kun k käy pystyrivit, 1 < k < n. Koska ai11ai22
ainn tarkasteltaessa tehdään taas (n × n)-taulukko, jossa merkitään X :llä
ruutuja (ik , k), kun k käy pystyrivit, 1 < k < n. Koska ai11ai22 ainn = a1j1a2j2
ainn = a1j1a2j2 anjn, on
saatu taulukko sama kuin edellä. Nyt lasketaan permutaation (i1,...,in) käännetyt parit
seuraavasti. Jokaisessa sarakkeessa merkitään O :lla niitä taulukon ruutuja, jotka ovat merkin X
yläpuolella ja joiden kanssa samalla rivillä oikealla ei ole merkkiä X. Merkkien O lukumäärä on
käännettyjen parien lukumäärä. Molemmilla tavoilla laskettaessa lasketaan tarkalleen
samat taulukon ruudut, joten sign(i1,...,in) = sign(j1,...,jn). Täten on saatu väite.
anjn, on
saatu taulukko sama kuin edellä. Nyt lasketaan permutaation (i1,...,in) käännetyt parit
seuraavasti. Jokaisessa sarakkeessa merkitään O :lla niitä taulukon ruutuja, jotka ovat merkin X
yläpuolella ja joiden kanssa samalla rivillä oikealla ei ole merkkiä X. Merkkien O lukumäärä on
käännettyjen parien lukumäärä. Molemmilla tavoilla laskettaessa lasketaan tarkalleen
samat taulukon ruudut, joten sign(i1,...,in) = sign(j1,...,jn). Täten on saatu väite. ![[]](images/msam10-c-3.gif)
